Bug Test¶

Bug Test 1¶

Add this line will cause bug \(\( \text { minimize } E[f]=E_{\text {field-aligned }}+\mu E_{\text {snap }}+\varepsilon E_{\text {reg }} \text { s.t. } f \text { is seamless } \)\)

\[ \text { minimize } E[f]=E_{\text {field-aligned }}+\mu E_{\text {snap }}+\varepsilon E_{\text {reg }} \text { s.t. } f \text { is seamless } \]

abcdefg

Bug Test 2¶

Parametrization¶

\[ \text { minimize } E[f]=E_{\text {field-aligned }}+\mu E_{\text {snap }}+\varepsilon E_{\text {reg }} \text { s.t. } f \text { is seamless } \]

\(E_{\text {field-aligned }}\): a frame should be mapped to the canonical frame, and have a parameter control how many strokes should be merged

\[ E_{\text {align }}=\sum_{T \in \mathcal{T}}\left\|\mathcal{J}_f \tilde{\phi}-\mathrm{I}\right\|_{\mathrm{F}}^2 \]

\(\mu E_{\text {snap }}\): snapping grid to the isoline (intuition: nearby strokes can be grouped together by assigning them to the same, quantized isoline of the parametrization.)
- 每个三角面片都有两个 direction \(u, v\) ，其中一个 direction 会被选择为 tangent direction
- 假设一个三角面片的 tangent direction 为 \(u ， u\) 要尽可能的靠近参数空间中的 isoline，另一个 direction 会被施加约束
- Additional integer variable \((i, j)\) : 表示参数空间中的 isoline
- 此项被定义为一个 soft constraint，使得 stroke 三角形的受约束参数受到其最近 integer variable 的吸引
- 注: 这里的 additional integer variable 并不是一个三角面片一个，而是决定好一个三角面片之后，周围的三角面片使用同样的 additional integer variable

\[ E_{\text {snap }}=\sum_{c \in \mathcal{C}_{\mathrm{c}}} w_{\text {snap }}\|u-\bar{u}\|^2+\sum_{c \in \mathcal{C}_t} w_{\text {snap }}\|v-\bar{v}\|^2 \]

Choose Tangent Direction
- trace the streamlines in each of the two frame field directions
- count the number of black pixels encountered by each streamline
- direction with more black pixels is the tangent direction
- Note: black dots correspond to cases when the two pixel counts are very close, in which cas we leave the triangle unlabelled and we don't use it for snapping
\(\varepsilon E_{r e g}:\) L2 regression

Bug test 3¶

Transformation¶

2D 线性变换¶

线性变换：变换能够用矩阵乘法得到

可以说，Linear Transformation = Matrices (of the same dimension)

我们将如下所示的简单矩阵乘法定义为对向量 \((x, y)^{T}\) 的线性变换。 \(\( \left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} a_{11} x+a_{12} y \\ a_{21} x+a_{22} y \end{array}\right] \)\)

缩放 (scale)¶

缩放变换是一种沿着坐标轴作用的变换，定义如下: \(\( \operatorname{scale}\left(s_{x}, s_{y}\right)=\left[\begin{array}{cc} s_{x} & 0 \\ 0 & s_{y} \end{array}\right] \)\) 即除了 \((0,0)^{T}\) 保持不变之外，所有的点变为 \(\left(s_{x} x, s_{y} y\right)^{T}\)

剪切 (shearing)¶

shear 变换直观理解就是把物体一边固定，然后拉另外一边，定义如下: \(\( shear-x(s)=\left[\begin{array}{ll}1 & s \\ 0 & 1\end{array}\right], \\shear-y (s)=\left[\begin{array}{ll}1 & 0 \\ s & 1\end{array}\right] \)\)

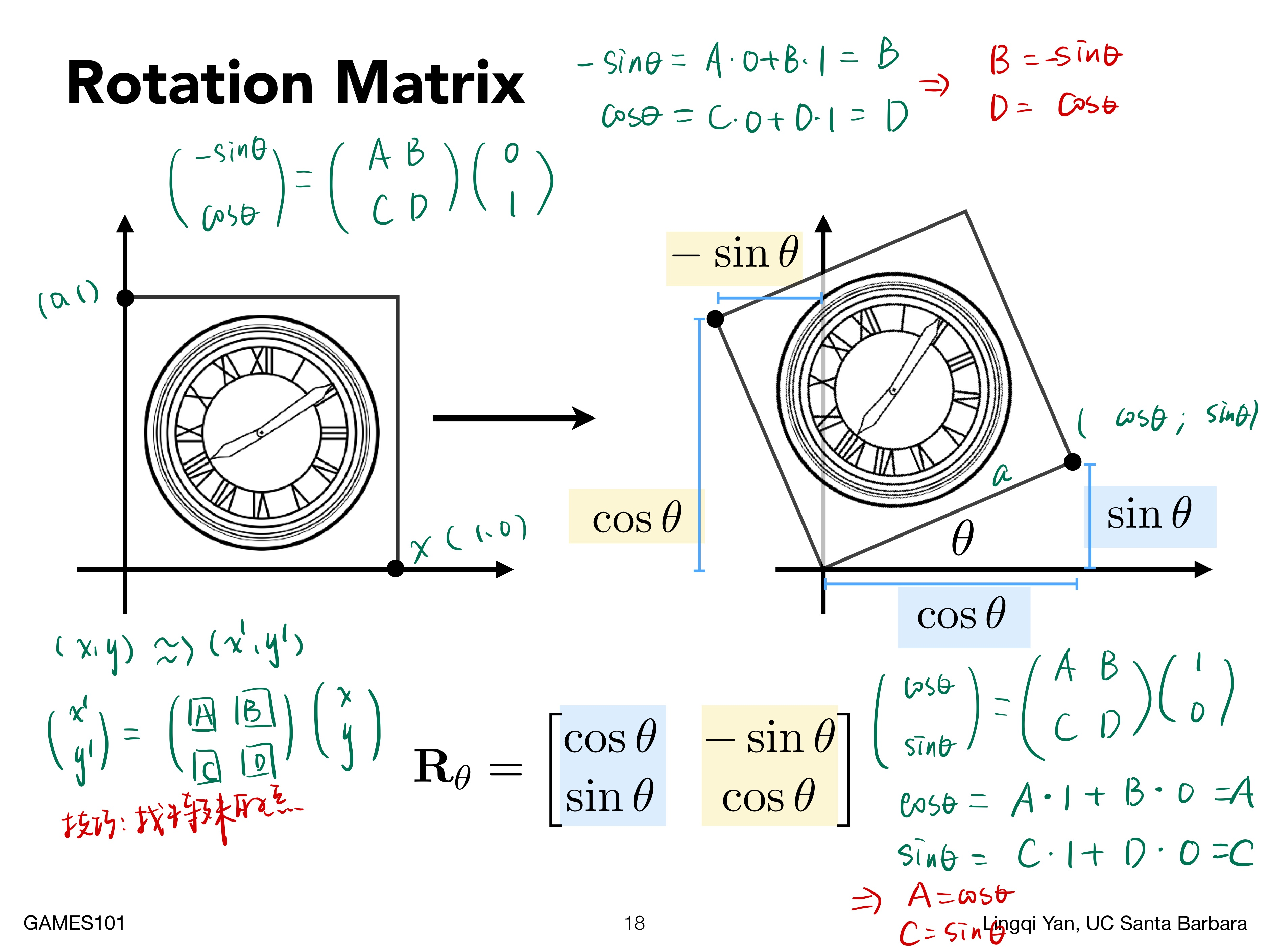
旋转 (rotation)¶

在无特殊说明的情况下，默认关于 \((0,0)\) 点，逆时针方向旋转 \(\theta\) 角度（弧度）的公式如下

\[ \mathbf{R}_{\theta}=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] \]

推导如下

¶

Scale¶

\[ \mathbf{S}\left(s_{x}, s_{y}\right)=\left(\begin{array}{ccc} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & 1 \end{array}\right) \]

Rotation¶

\[ \mathbf{R}(\alpha)=\left(\begin{array}{ccc} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{array}\right) \]

Translation¶

\[ \mathbf{T}\left(t_{x}, t_{y}\right)=\left(\begin{array}{ccc} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{array}\right) \]

Use \(4 \times 4\) matrices for affine transformations \(\( \left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{lllc} a & b & c & t_{x} \\ d & e & f & t_{y} \\ g & h & i & t_{z} \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right) \)\)

Scale¶

\[ \mathbf{S}\left(s_{x}, s_{y}, s_{z}\right)=\left(\begin{array}{cccc} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \]

Translation¶

\[ \mathbf{T}\left(t_{x}, t_{y}, t_{z}\right)=\left(\begin{array}{cccc} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{array}\right) \]

\[ \begin{aligned} \mathbf{R}_{x}(\alpha) &=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \\ \mathbf{R}_{y}(\alpha) &=\left(\begin{array}{cccc} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \\ \mathbf{R}_{z}(\alpha) &=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \end{aligned} \]

Rodrigues’ Rotation Formula¶

Rotation by angle \(\alpha\) around axis \(n\) \(\( \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{array}\right)}_{\mathbf{N}} \)\)

正则投影的变换矩阵¶

Translate (center to origin) first, then scale (length/width/height to 2) \(\( M_{\text {ortho }}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right] \)\)

透视投影的变换矩阵推导¶

计算机图形学二：视图变换(坐标系转化，正交投影，透视投影，视口变换)

透视投影的变换矩阵¶

\[ \mathrm{M}_{\text {per }}=\mathrm{M}_{\text {ortho }} \mathrm{M}_{\text {persp } \rightarrow\text { ortho }} \]

\[ \mathrm{M}_{\text {per }}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -f n \\ 0 & 0 & 1 & 0 \end{array}\right] \]

Last update: July 27, 2023
Created: June 16, 2023