Skip to content

Lecture 17 Materials and Appearances

Material = BRDF

Diffuse / Lambertian Material

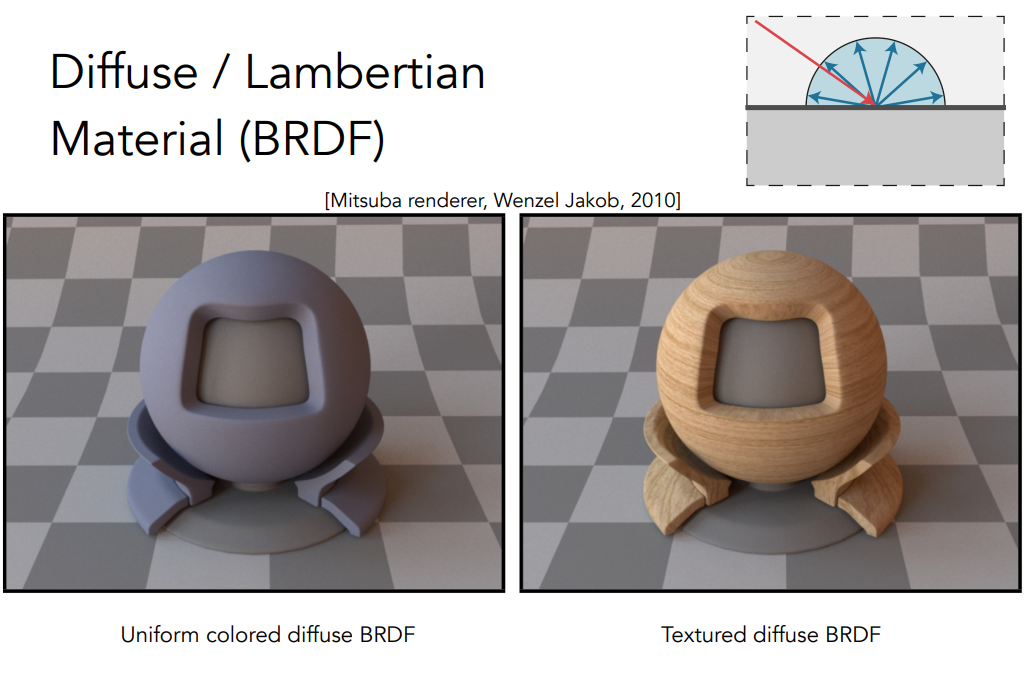
image-20221119204045439

Light is equally reflected in each output direction

Suppose the incident lighting is uniform（均匀的）and diffuse \(\to\) 入射的 Irradiance= 出射的 Irradiance \(\to\) 入射的 radiance= 出射的 radiance

这样就可以写出渲染方程，没有自己发光项

简化渲染方程，假设入射的 radiance 为常数，BRDF 为常数，结果就是对半球上的一个 \(\cos\theta\) 函数的积分 \(\to \ \pi\)

\[ \begin{aligned} L_o\left(\omega_o\right) &=\int_{H^2} f_r L_i\left(\omega_i\right) \cos \theta_i \mathrm{~d} \omega_i \\ &=f_r L_i \int_{H^2} \cos \theta_i \mathrm{~d} \omega_i \\ &=\pi f_r L_i \end{aligned} \]

由于能量守恒，入射的 radiance= 出射的 radiance，即 \(L_i = L_o\)，所以有

\[ \text{BRDF}=f_r = \frac{1}{\pi} \]
  • albedo (color) [反射率，可以引入不同的颜色]
\[ f_r=\frac{\rho}{\pi} \]

image-20221119114803691

Glossy material (BRDF)

image-20221119204101265

Ideal reflective / refractive material (BSDF*)

  • 双向散射分布函数 (Bidirectional scattering distribution function)

image-20221119204119019

Specular Refraction

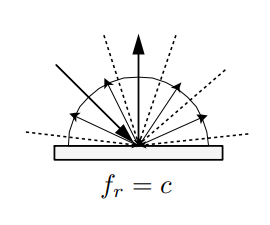
Perfect Specular Reflection

  • 性质：入射光和出射光的角平分线一定是法线

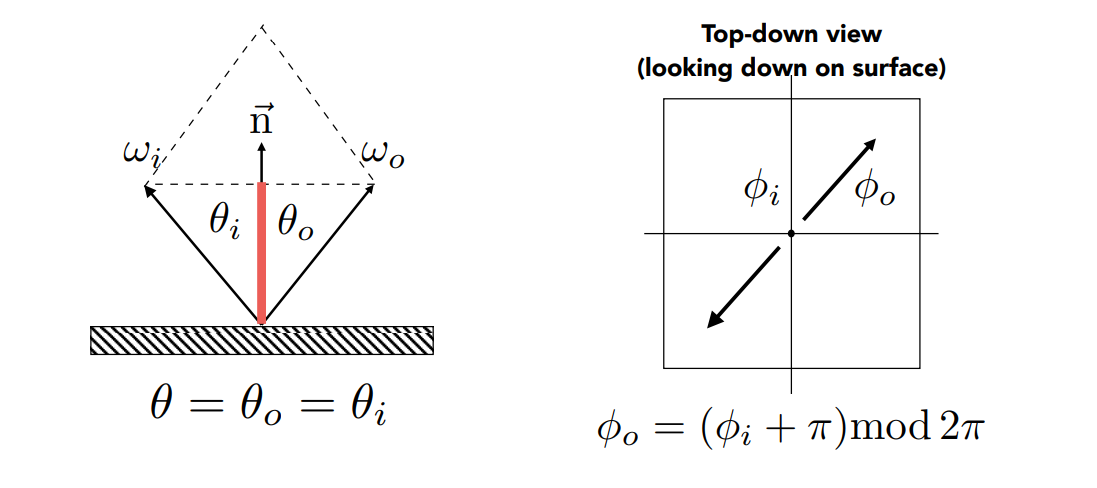
image-20221119204330472

\[ \begin{aligned} &\omega_o+\omega_i=2 \cos \theta \overrightarrow{\mathrm{n}}=2\left(\omega_i \cdot \overrightarrow{\mathrm{n}}\right) \overrightarrow{\mathrm{n}} \\ &\omega_o=-\omega_i+2\left(\omega_i \cdot \overrightarrow{\mathrm{n}}\right) \overrightarrow{\mathrm{n}} \end{aligned} \]

Snell’s Law

  • 也叫折射定律
  • Transmitted angle depends on
    • index of refraction (IOR) for incident ray
    • index of refraction (IOR) for exiting ray

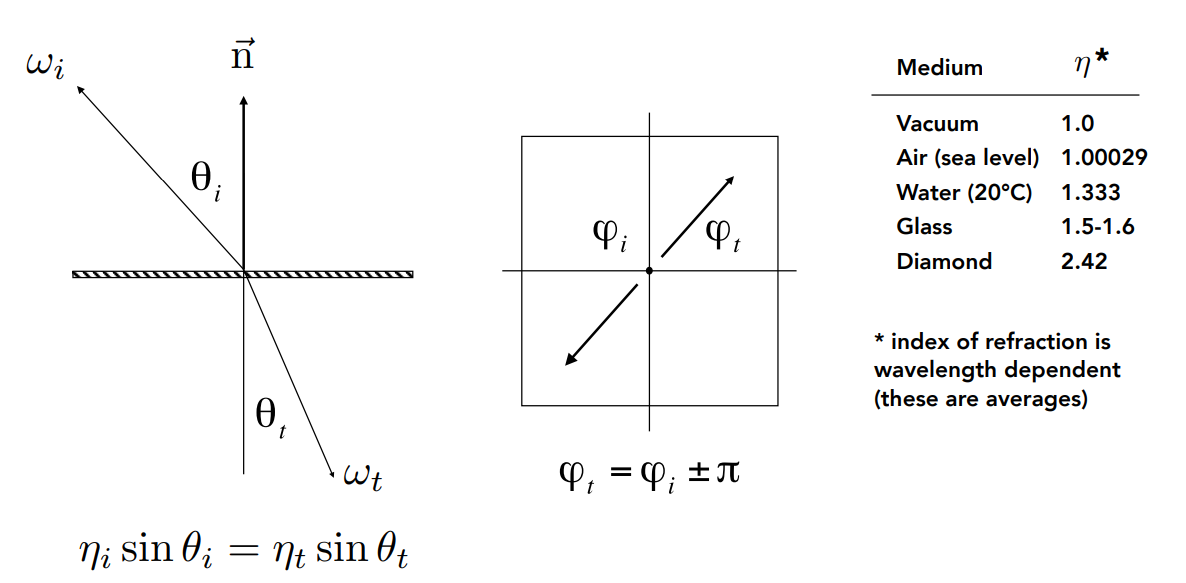
image-20221119205232326

Law of Refraction

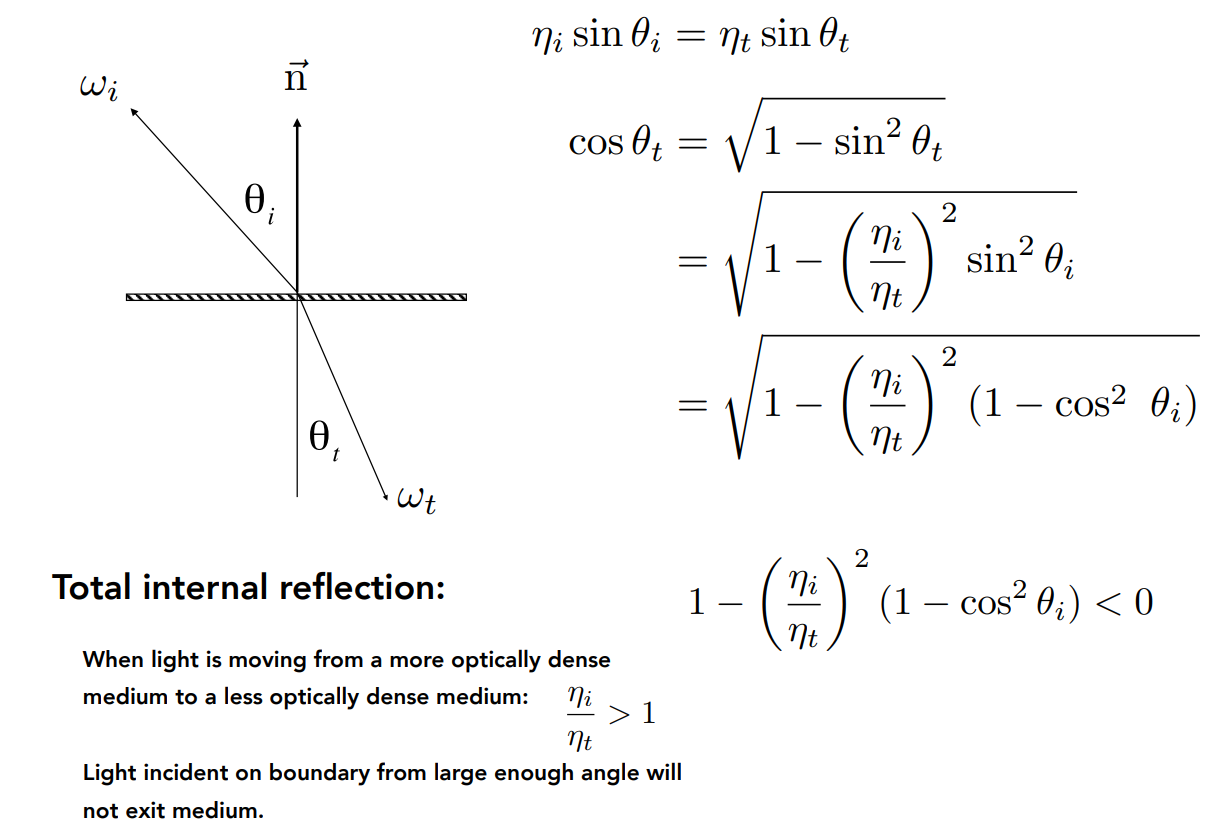
image-20221119205420759

  • 折射不可能发射的情况：When light is moving from a more optically dense medium to a less optically dense medium (i.e. \(\frac{\eta_i}{\eta_t}>1\)) Light incident on boundary from large enough angle will not exit medium.

Fresnel Reflection / Term

  • reflectance increases with grazing angle

image-20221119230241943

Fresnel Term — Formulae

  • Accurate: need to consider polarization 考虑光的两个极化
\[ \begin{aligned} &R_{\mathrm{s}}=\left|\frac{n_1 \cos \theta_{\mathrm{i}}-n_2 \cos \theta_{\mathrm{t}}}{n_1 \cos \theta_{\mathrm{i}}+n_2 \cos \theta_{\mathrm{t}}}\right|^2=\left|\frac{n_1 \cos \theta_{\mathrm{i}}-n_2 \sqrt{1-\left(\frac{n_1}{n_2} \sin \theta_{\mathrm{i}}\right)^2}}{n_1 \cos \theta_{\mathrm{i}}+n_2 \sqrt{1-\left(\frac{n_1}{n_2} \sin \theta_{\mathrm{i}}\right)^2}}\right|^2, \\ &R_{\mathrm{p}}=\left|\frac{n_1 \cos \theta_{\mathrm{t}}-n_2 \cos \theta_{\mathrm{i}}}{n_1 \cos \theta_{\mathrm{t}}+n_2 \cos \theta_{\mathrm{i}}}\right|^2=\left|\frac{n_1 \sqrt{1-\left(\frac{n_1}{n_2} \sin \theta_{\mathrm{i}}\right)^2}-n_2 \cos \theta_{\mathrm{i}}}{n_1 \sqrt{1-\left(\frac{n_1}{n_2} \sin \theta_{\mathrm{i}}\right)^2}+n_2 \cos \theta_{\mathrm{i}}}\right|^2 . \end{aligned} \]

再取它们的平均即可，即

\[ R_{\mathrm{eff}}=\frac{1}{2}\left(R_{\mathrm{s}}+R_{\mathrm{p}}\right) \]

  • Approximate: Schlick’s approximation

    • 对刚刚的精确公式拟合一个曲线，设基准反射率为 \(R_0\)
\[ \begin{aligned} R(\theta) &=R_0+\left(1-R_0\right)(1-\cos \theta)^5 \\ R_0 &=\left(\frac{n_1-n_2}{n_1+n_2}\right)^2 \end{aligned} \]

Microfacet Material

  • Name: 微表面模型
  • 观察者从远处看的时候，看到的粗糙表面成为平的表面，看到的是材质
  • 观察者从近处看的时候，看到的是几何

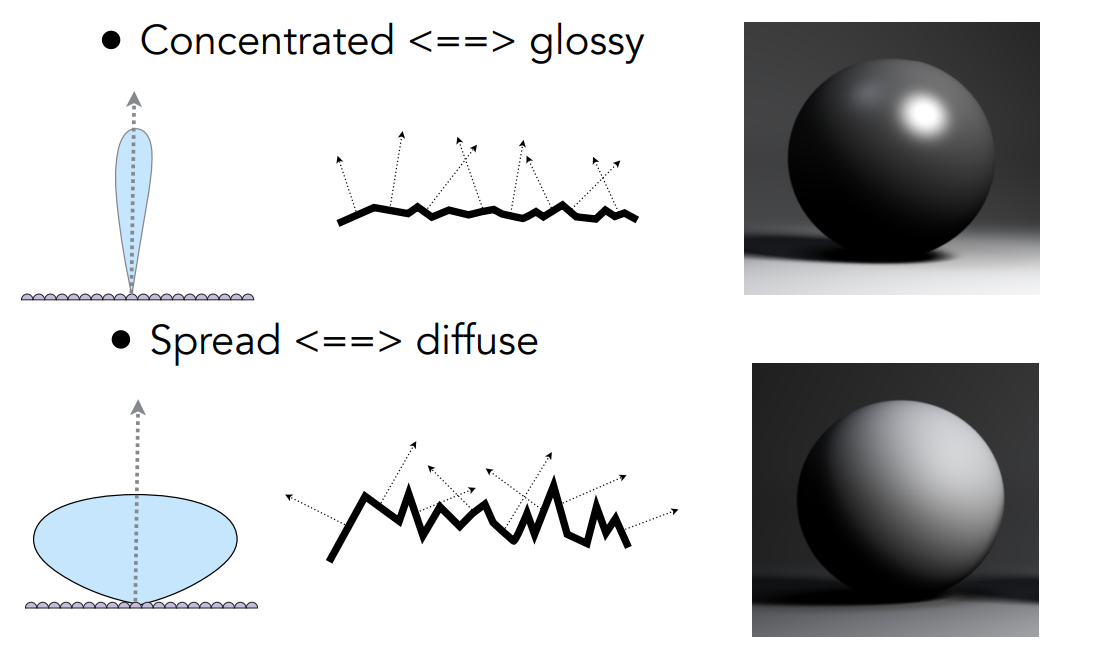
Rough surface

  • Macroscale: flat & rough
  • Microscale: bumpy & specular

Individual elements of surface act like mirrors （每一个微表面可以认为是镜面）

  • Known as Microfacets
  • Each microfacet has its own normal

Microfacet BRDF

  • Key: the distribution of microfacets’ normals
  • 通过微表面模型，可以把表面的粗糙程度用表面的法线分布表示

image-20221119231530569

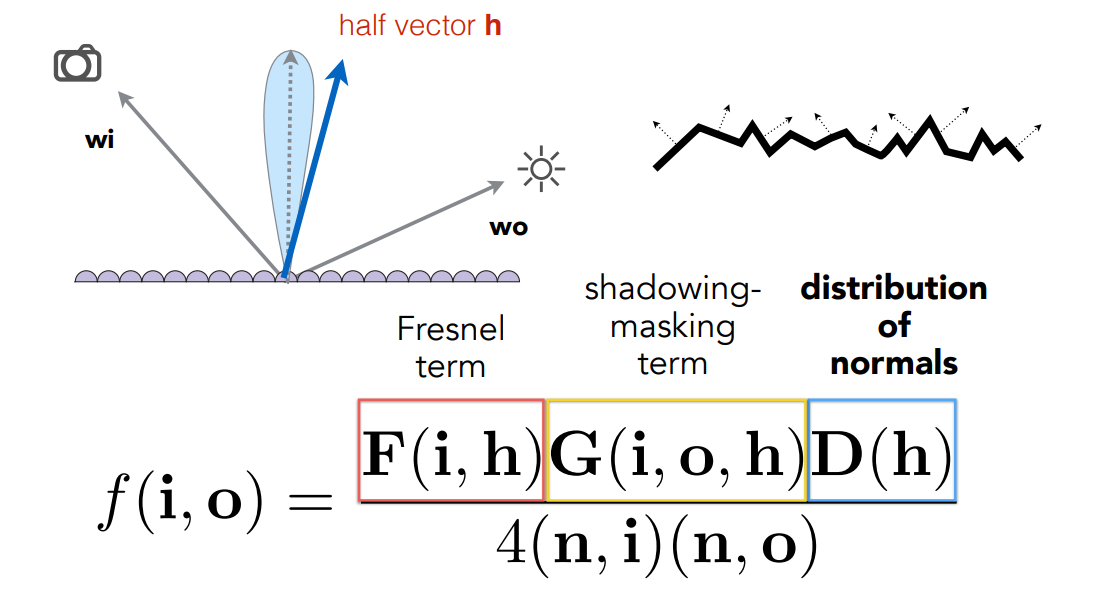
image-20221119231629340

  • \(F(i,h)\): 表示菲涅尔项，总共有多少能量被反射
  • \(G(i,o,h)\): 几何项，微表面可能互相遮挡（自己给自己的阴影）导致有一些微表面失去了它的作用
    • 光方向与物体表面几乎平行的时候最明显，Grazing Angel
  • \(D(h)\): 表示微表面的法线分布，因为每一个微表面都可以认为是镜面，只有半程向量和法线垂直的微表面能够将光反射到出射方向

Isotropic / Anisotropic Materials (BRDFs)

  • Isotropic 各向同性：微表面不存在方向性或者方向性很弱

  • Anisotropic 各向异性：微表面存在方向性

    • 识别：BRDF 在方位上旋转得到相同的 BRDF

    • Reflection depends on azimuthal angle \(\phi\)

    \[ f_r\left(\theta_i, \phi_i ; \theta_r, \phi_r\right) \neq f_r\left(\theta_i, \theta_r, \phi_r-\phi_i\right) \]
    • Example

    image-20221119233620355

image-20221119233353400

Properties of BRDFs

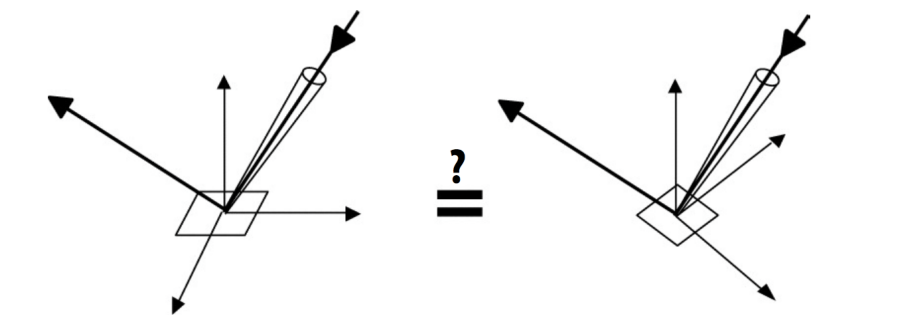
  • Non-negativity
\[ f_r\left(\omega_i \rightarrow \omega_r\right) \geq 0 \]
  • Linearity 线性性质（可以加起来）
\[ L_r\left(\mathrm{p}, \omega_r\right)=\int_{H^2} f_r\left(\mathrm{p}, \omega_i \rightarrow \omega_r\right) L_i\left(\mathrm{p}, \omega_i\right) \cos \theta_i \mathrm{~d} \omega_i \]

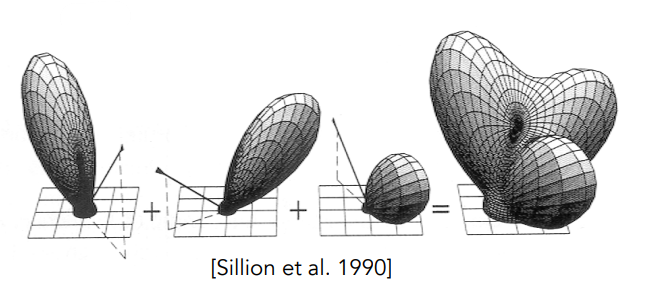
image-20221119234031903

  • Reciprocity principle 可逆性（交换入射方向和出射方向的角色，得到的 BRDF 相同）
\[ f_r\left(\omega_r \rightarrow \omega_i\right)=f_r\left(\omega_i \rightarrow \omega_r\right) \]

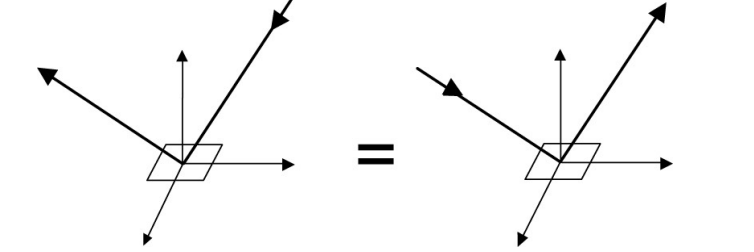
image-20221119234139136

  • Energy conservation 能量守恒
    • 在 Path Tracing 时经过无限次的光线弹射，最后的光线收敛就是因为能量守恒
\[ \forall \omega_r \int_{H^2} f_r\left(\omega_i \rightarrow \omega_r\right) \cos \theta_i \mathrm{~d} \omega_i \leq 1 \]

  • Isotropic vs. anisotropic

    • If isotropic, \(f_r\left(\theta_i, \phi_i ; \theta_r, \phi_r\right)=f_r\left(\theta_i, \theta_r, \phi_r-\phi_i\right)\)

    • 各向同性意味着 BRDF 之和相对的方位角有关，实际上此时 \(f_r\) 为三维

    • Then, from reciprocity,

    • 相对的方位角不用考虑正负 \(\to\) BRDF 的测量与储存

    \[ f_r\left(\theta_i, \theta_r, \phi_r-\phi_i\right)=f_r\left(\theta_r, \theta_i, \phi_i-\phi_r\right)=f_r\left(\theta_i, \theta_r,\left|\phi_r-\phi_i\right|\right) \]

image-20221119234526364

Measuring BRDFs

Measuring BRDFs: Motivation

Avoid need to develop / derive models - Automatically includes all of the scattering effects present

Can accurately render with real-world materials

  • Useful for product design, special effects, ...

Image-Based BRDF Measurement

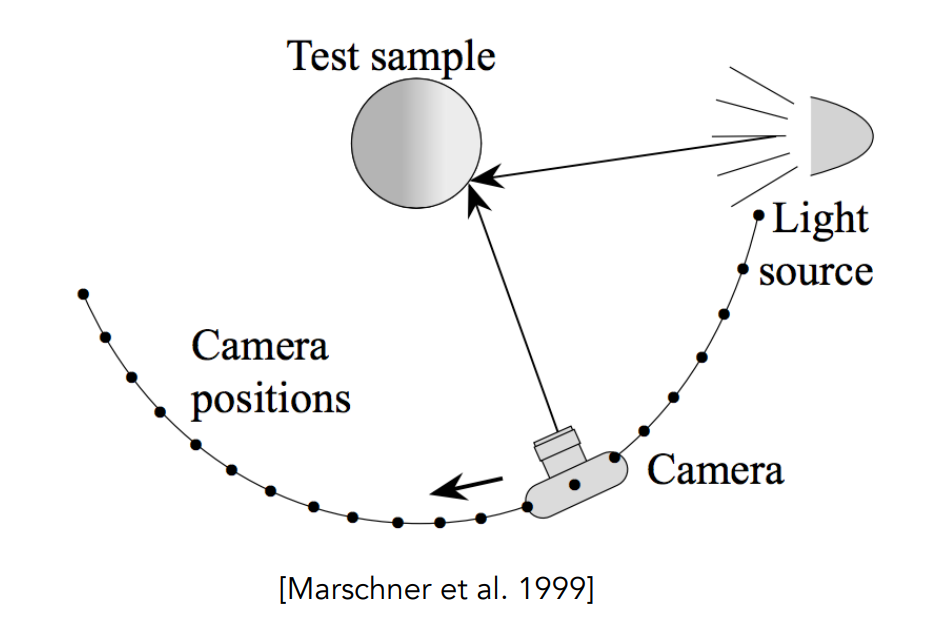
image-20221119234801879

  • Algorithm
for each outgoing direction wo
    move light to illuminate surface with a thin beam from wo
    for each incoming direction wi
    move sensor to be at direction wi from surface
    measure incident radiance

Improving efficiency: - Isotropic surfaces reduce dimensionality from 4D to 3D - Reciprocity reduces # of measurements by half - Clever optical systems... (例如猜出来)

Challenges in Measuring BRDFs

  • Accurate measurements at grazing angles
    • Important due to Fresnel effects
  • Measuring with dense enough sampling to capture high frequency specularities
  • Retro-reflection
  • Spatially-varying reflectance, ...

Representing Measured BRDFs

Desirable qualities - Compact representation - Accurate representation of measured data - Efficient evaluation for arbitrary pairs of directions - Good distributions available for importance sampling

Tabular Representation

Store regularly-spaced samples in \(\( \left(\theta_i, \theta_o,\left|\phi_i-\phi_o\right|\right) \)\) - Better: reparameterize angles to better match specularities

image-20221119235348515

Last update: July 30, 2023
Created: June 16, 2023