Lecture 13-16 Ray Tracing¶

Why Ray Tracing¶

光栅化不能得到很好的全局光照效果
- 软阴影
- 光线弹射超过一次（间接光照）
光栅化是一个快速的近似，但是质量较低

光线追踪是准确的，但是较慢
- Rasterization: real-time, ray tracing: offline
- 生成一帧需要一万CPU小时

Basic Ray-Tracing Algorithm¶

图形学上的光线定义
- 光线是沿直线传播的
- 两个或多个光线不会发生碰撞
- 光线一定会从光源出发到达我们的眼镜
- light reciprocity 光路的可逆性

Pinhole Camera Model¶

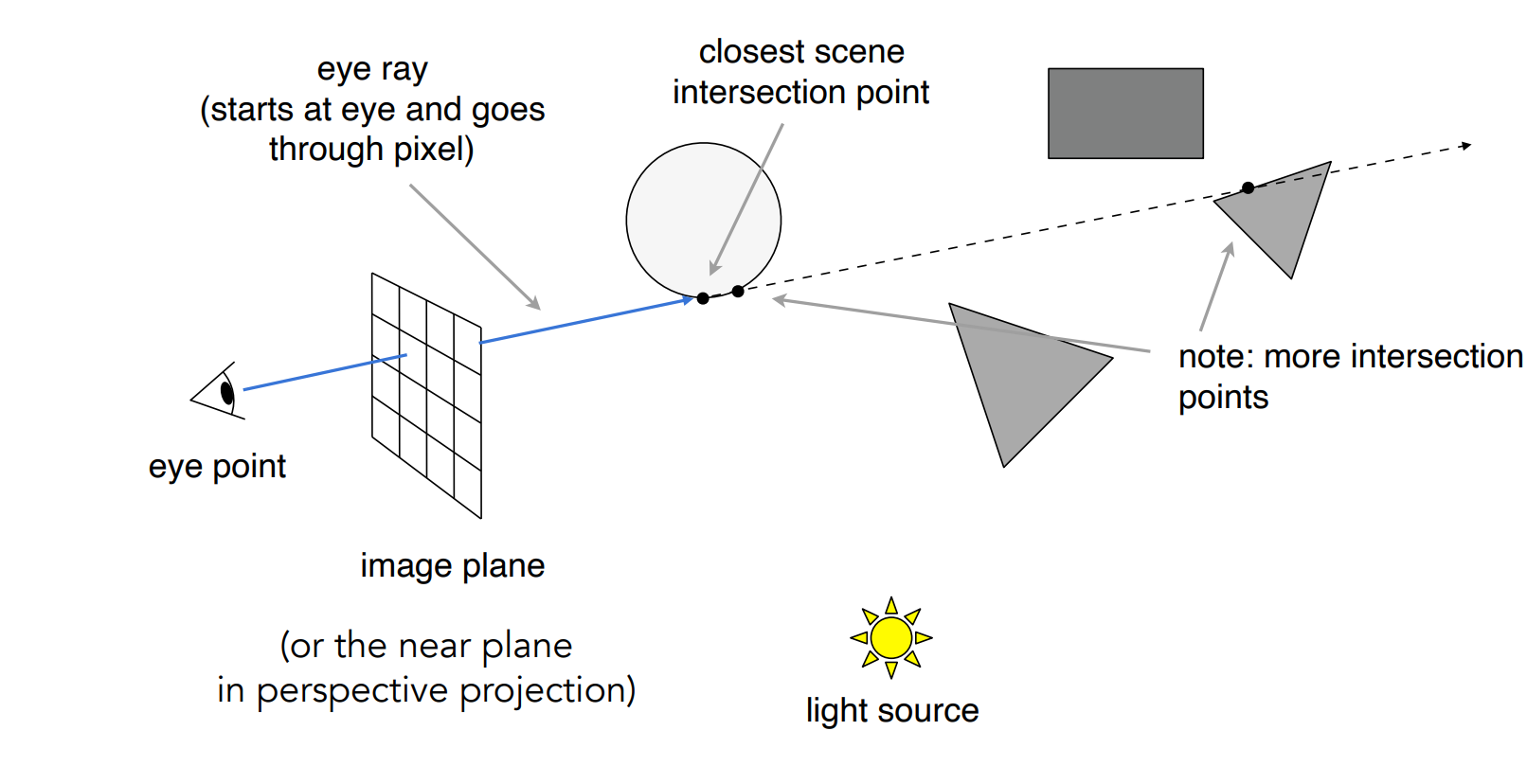
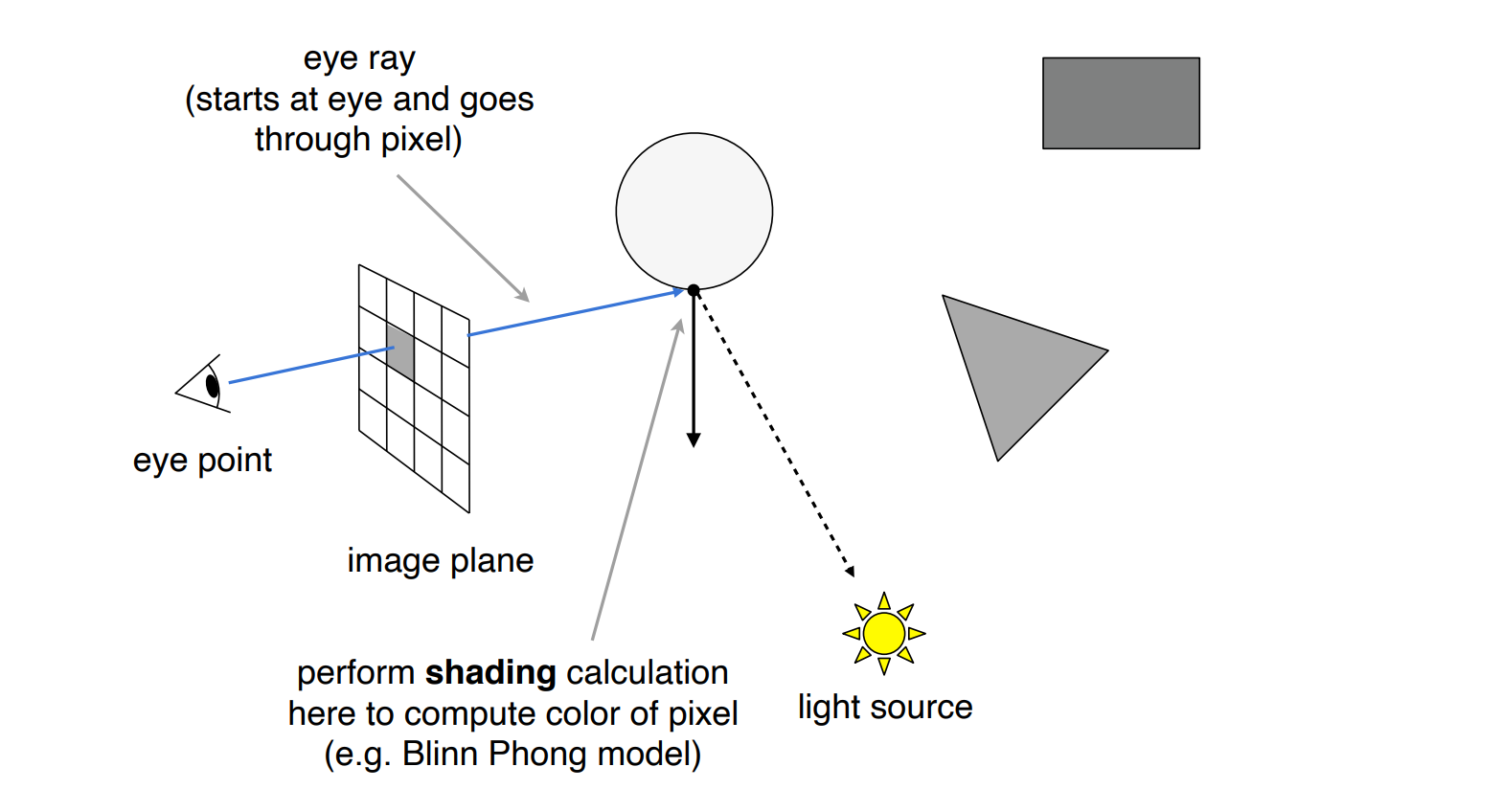
对于每一个像素，从眼睛投射出一个光线（eye ray）
和场景相交，求最近的交点
和光源连线判断是否对光源可见
计算着色，写回像素的值

以上算法还是只考虑了光线只弹射一次的情况

Recursive (Whitted-Style) Ray Tracing¶

在任意一个点可以继续传播光线（反射和折射）
所有点的着色都会被加到像素中（需要计算能量损失）

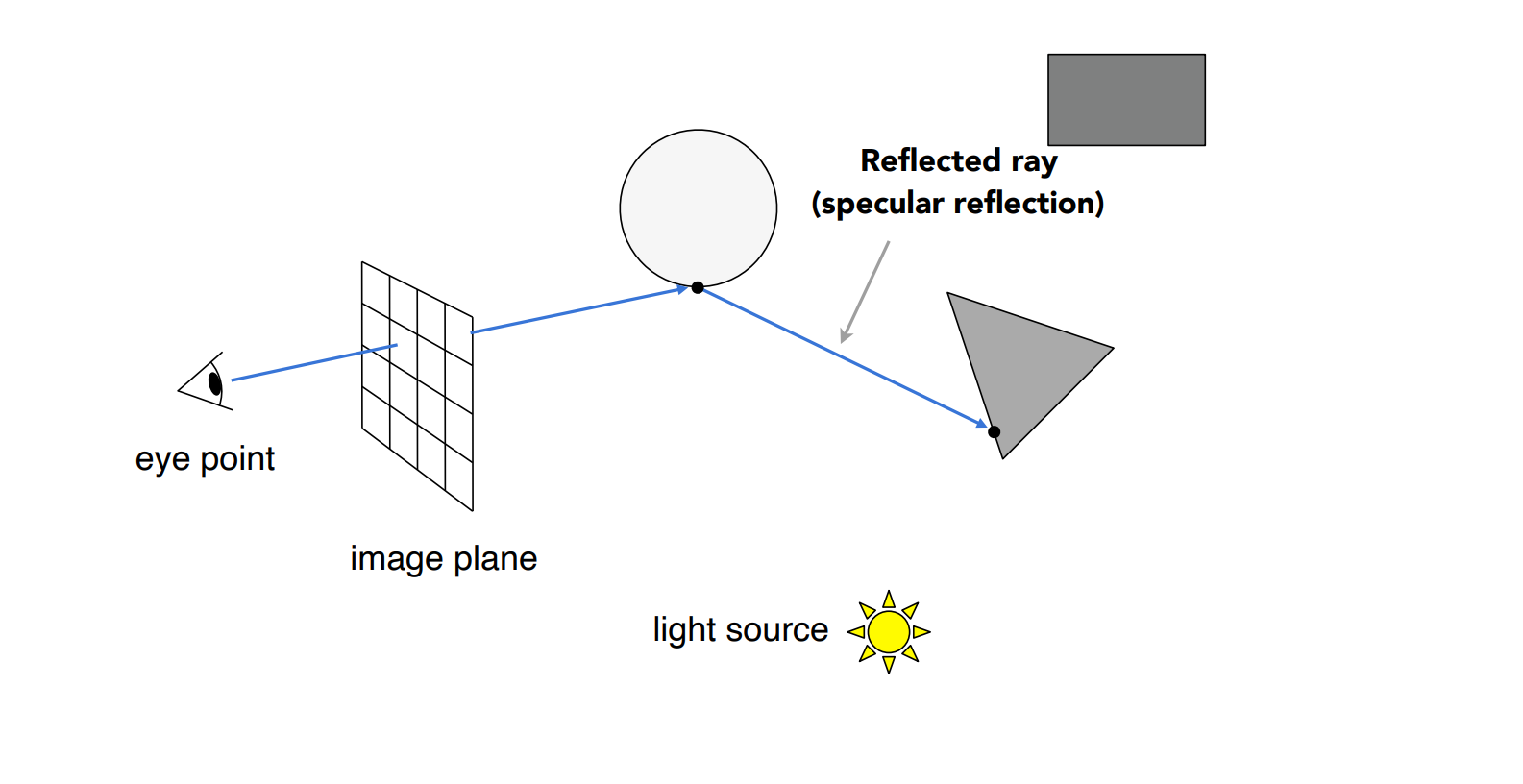
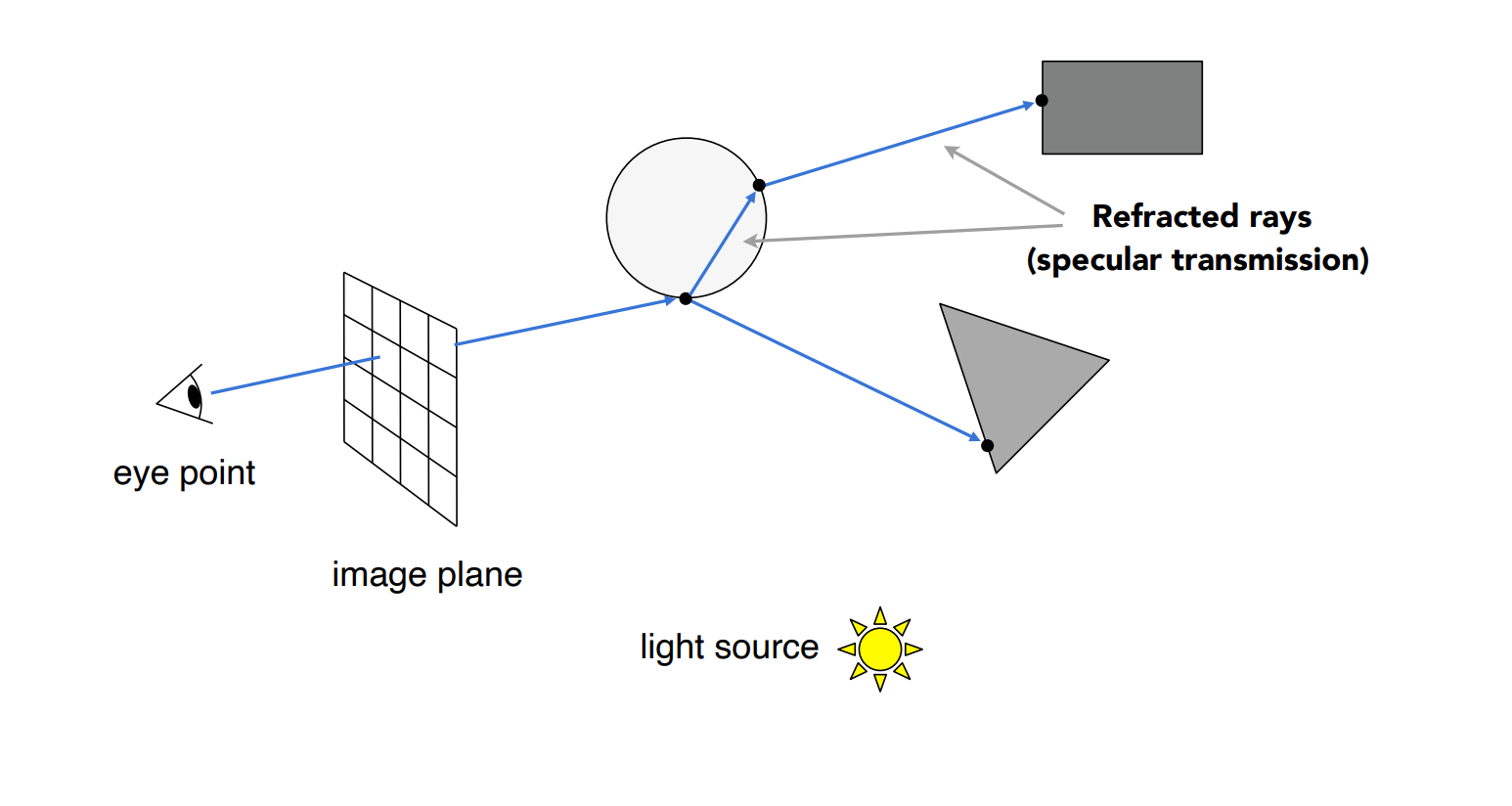
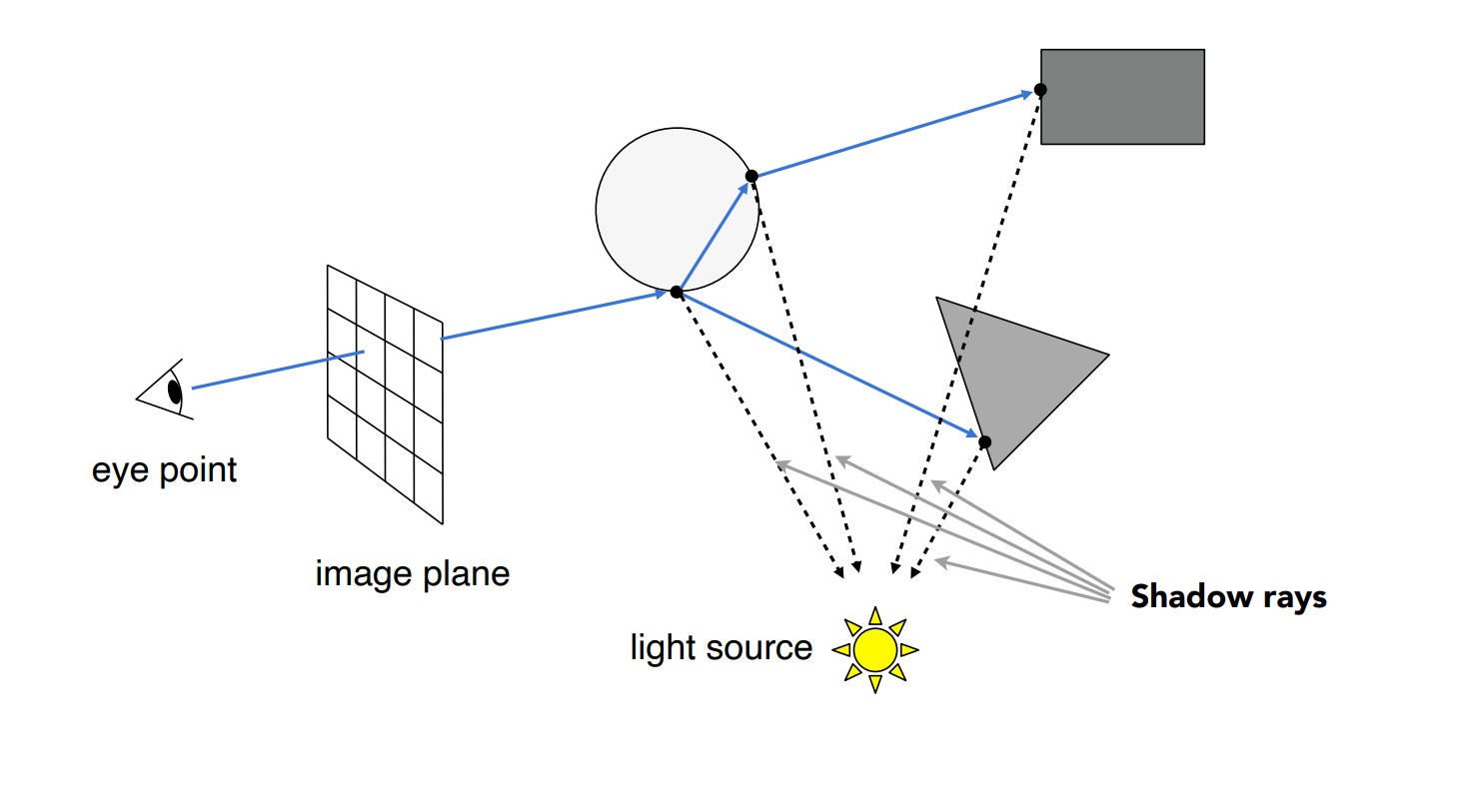
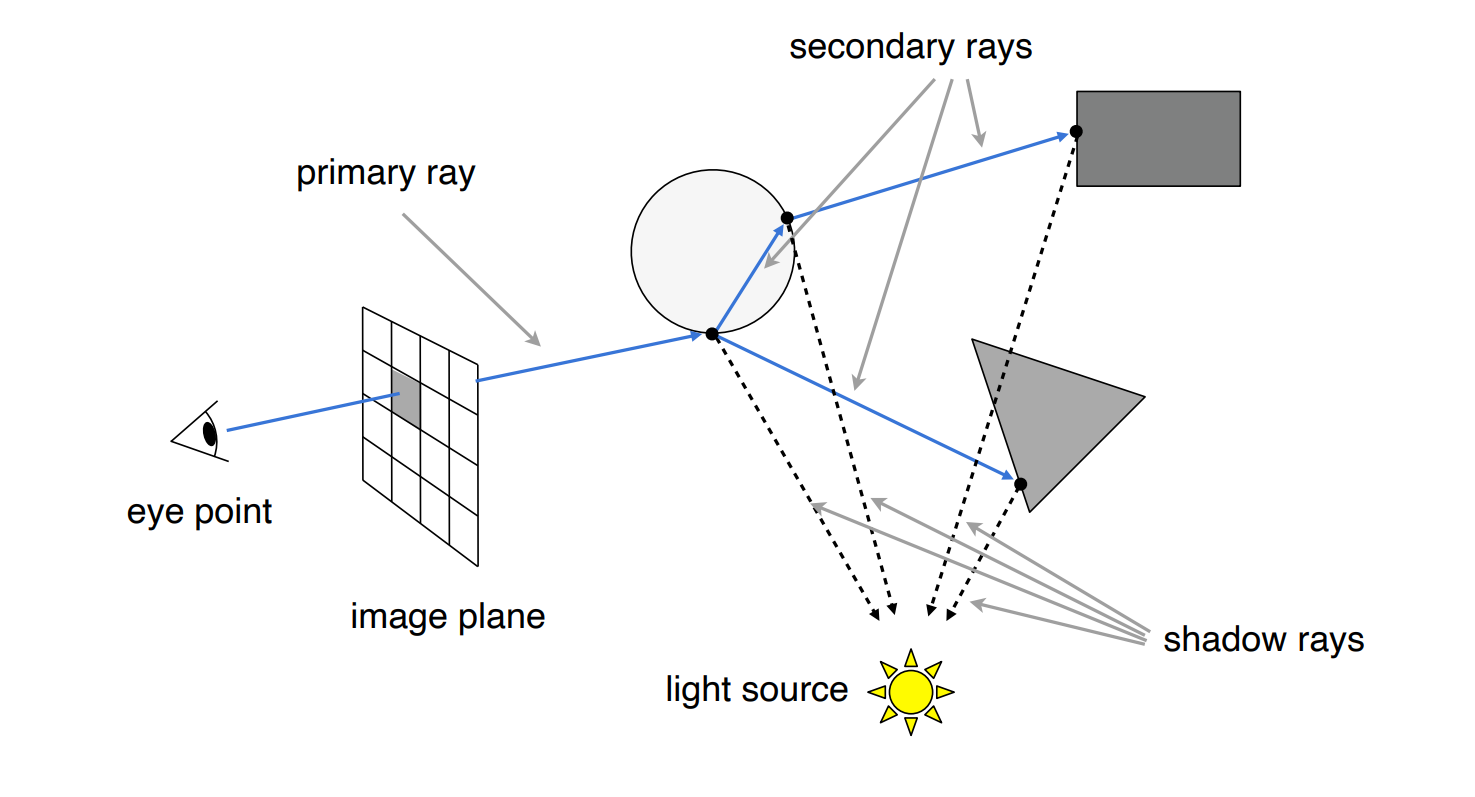
对于从眼睛出发的光线定义为 Primary Ray
由 Primary Ray 折射和反射的光线可以称作 Secondary Ray
判断可见性的光路被称作 Shadow Ray

Ray-Surface Intersection¶

Ray Equation¶

光线被定义为有一个起点和方向的向量
Equation: \(\mathbf{r}(t)=\mathbf{o}+t \mathbf{d}, 0 \leq t<\infty\)

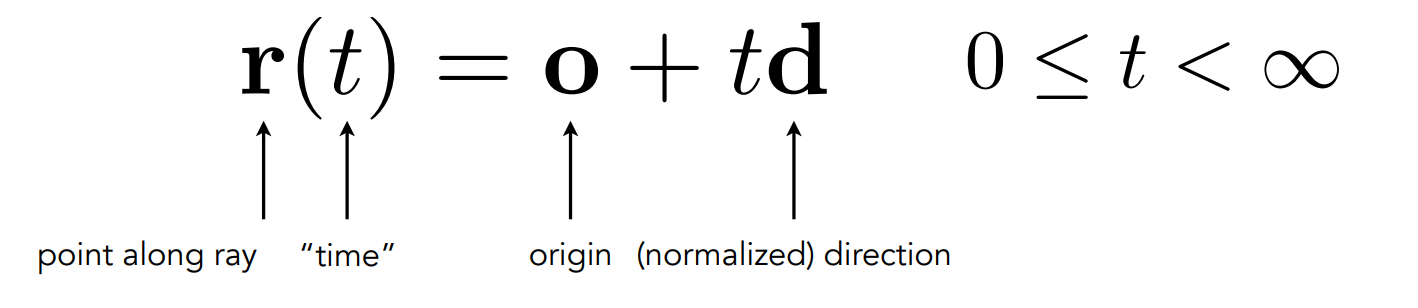
Ray Intersection With Sphere¶

Ray: \(\mathbf{r}(t)=\mathbf{o}+t \mathbf{d}, 0 \leq t<\infty\)
Sphere: \(\mathbf{p}:(\mathbf{p}-\mathbf{c})^2-R^2=0\)

由于点需要满足两个方程，所以

\[ (\mathbf{o}+t \mathbf{d}-\mathbf{c})^2-R^2=0 \]

展开后也就有，

\[ \begin{aligned} &a t^2+b t+c=0, \text { where } \\ &a=\mathbf{d} \cdot \mathbf{d} \\ &b=2(\mathbf{o}-\mathbf{c}) \cdot \mathbf{d} \\ &c=(\mathbf{o}-\mathbf{c}) \cdot(\mathbf{o}-\mathbf{c})-R^2 \\ &t=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a} \end{aligned} \]

注意，对于解出后的结果 \(t\)，需要满足 \(t\ge 0\)

Ray Intersection With Implicit Surface¶

Ray: \(\mathbf{r}(t)=\mathbf{o}+t \mathbf{d}, 0 \leq t<\infty\)

对于任意的隐式表面，有

General implicit surface: \(\mathbf{p}: f(\mathbf{p})=0\)
Substitute ray equation: \(f(\mathbf{o}+t \mathbf{d})=0\)

解出 Substitute ray equation 即可

注意，解出的结果需要是实数并且为非负数

Ray Intersection With Triangle Mesh¶

Convert It to Ray Intersection With Plane¶

Applications
- Rendering: visibility, shadows, lighting
- Geometry: inside/outside test （计算是否一个点是否在形状内部或者是外部，封闭物体）
- 在形状上取一个点找一个光线求交点，如果是奇数个交点，那么点就一定在物体内，否则在物体外
Compute
- Simple idea: just intersect ray with each triangle [Simple, but slow (acceleration?) ]
- Acceleration: 将光线和三角形求交转化为光线和平面求交，然后再判定交点是否在三角形内

Plane Equation¶

Plane is defined by normal vector and a point on plane

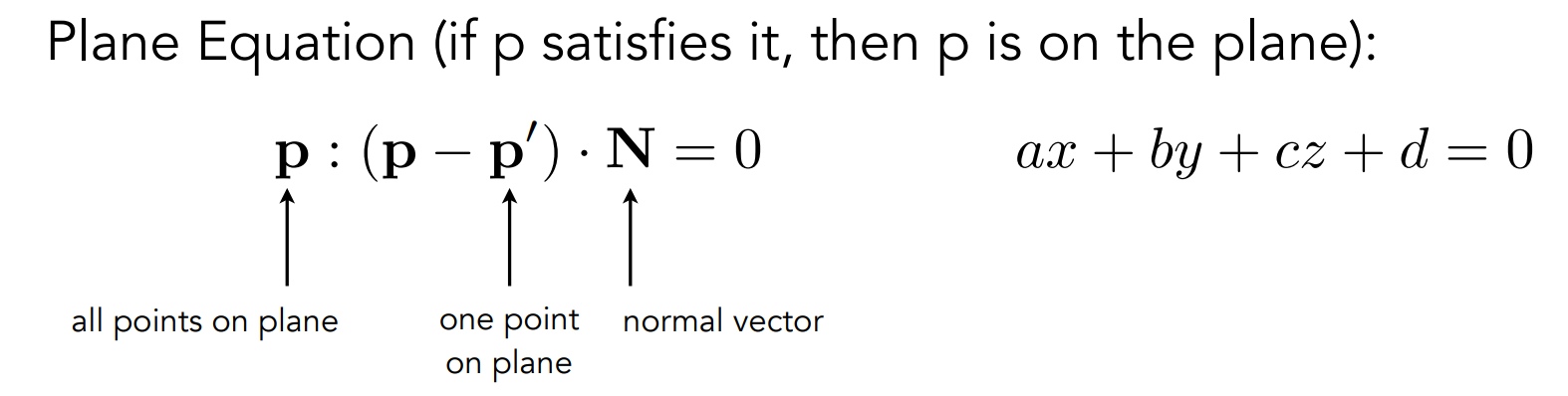
Ray Intersection With Plane¶

Ray equation: \(\mathbf{r}(t)=\mathbf{o}+t \mathbf{d}, 0 \leq t<\infty\)
Plane equation: \(\mathbf{p}:\left(\mathbf{p}-\mathbf{p}^{\prime}\right) \cdot \mathbf{N}=0\)
Solve for intersection

\[ \begin{aligned} & \text{set}\ \mathbf{p}=\mathbf{r}(t) \ \text{and solve for}\ t\\ &\left(\mathbf{p}-\mathbf{p}^{\prime}\right) \cdot \mathbf{N}=\left(\mathbf{o}+t \mathbf{d}-\mathbf{p}^{\prime}\right) \cdot \mathbf{N}=0 \\ &t=\frac{\left(\mathbf{p}^{\prime}-\mathbf{o}\right) \cdot \mathbf{N}}{\mathbf{d} \cdot \mathbf{N}} \end{aligned} \]

Check: \(0 \leq t<\infty\)，判断这个点是否在三角形内

Möller Trumbore Algorithm¶

A faster approach, giving barycentric coordinate directly （以另外一个形式描述平面）

\[ \overrightarrow{\mathbf{O}}+t \overrightarrow{\mathbf{D}}=\left(1-b_1-b_2\right) \overrightarrow{\mathbf{P}}_0+b_1 \overrightarrow{\mathbf{P}}_1+b_2 \overrightarrow{\mathbf{P}}_2 \]

联立光线和重心坐标
使用克莱姆法则解这个线性方程组，解出 \(b_1,b_2,t\)
如果 \(1-b_1-b_2, b_1, b_2\) 都是非负的，那么点在三角形内

Accelerating Ray-Surface Intersection¶

Simple ray-scene intersection
- Exhaustively test ray-intersection with every triangle
- Find the closest hit (i.e. minimum t)
Problem
- Naive algorithm = #pixels ⨉ # triangles (⨉ #bounces)
- Slow!!!

Bounding Volumes¶

Quick way to avoid intersections: bound complex object with a simple volume
- Object is fully contained in the volume
- If it doesn’t hit the volume, it doesn’t hit the object
- So test BVol first, then test object if it hits (如果一个光线连包围盒都碰不到，就也不可能碰到里面的物体)
Understanding: box is the intersection of 3 pairs of slabs (认为长方体是三组对面形成的交集)
Specifically: We often use an Axis-Aligned Bounding Box (AABB) [轴对齐包围盒]

Ray Intersection with Axis-Aligned Box¶

考虑二维的情况（两组对面）: Compute intersections with slabs and take intersection of \(t_{min}/t_{max}\) intervals
- 对得到的两组线段求交集即可

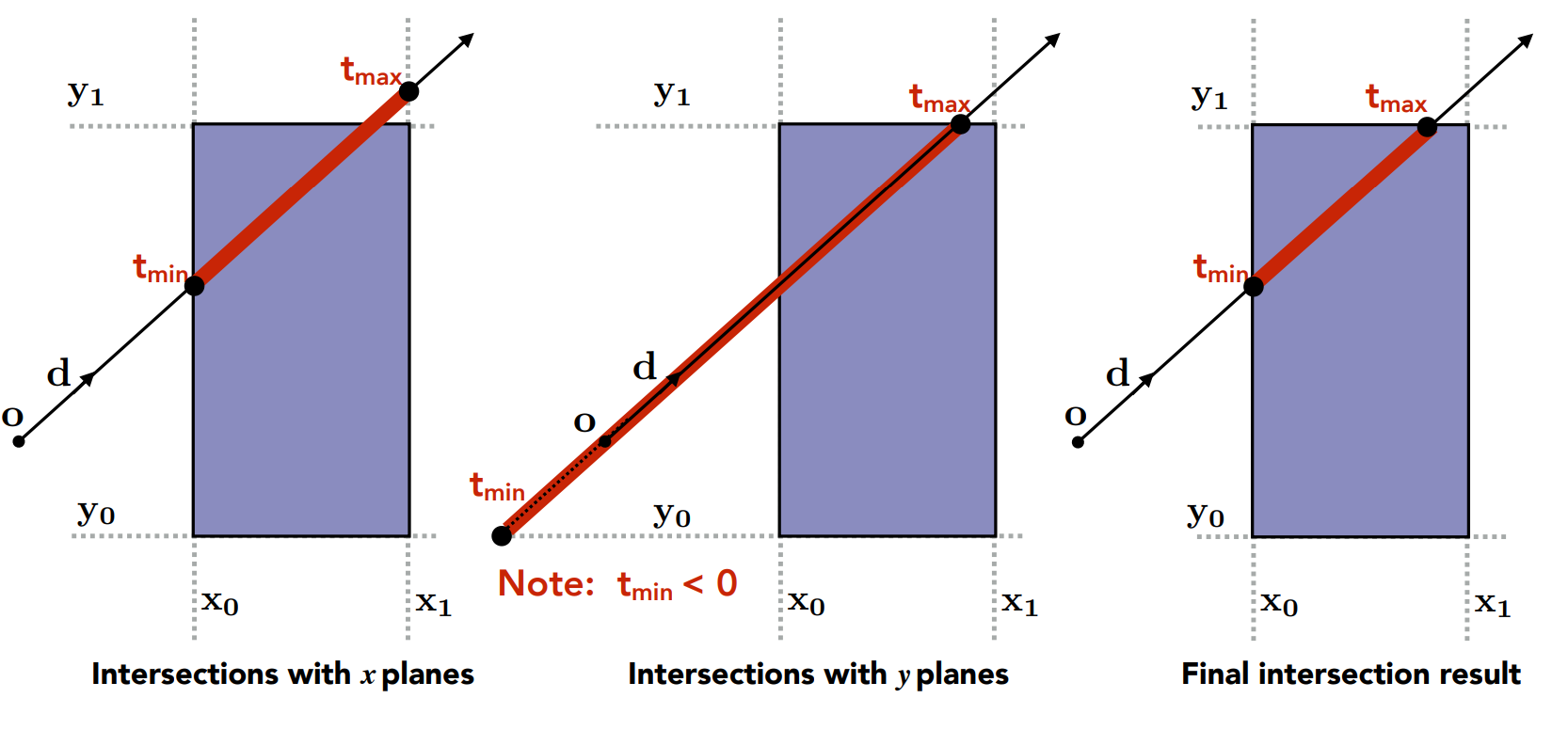
Recall: a box (3D) = three pairs of infinitely large slabs
Key ideas
- The ray enters the box only when it enters all pairs of slabs（如果三个对面都有光线进入，才能说光线进入了盒子）
- The ray exits the box as long as it exits any pair of slabs （只要光线离开任意一个对面，光线就算离开了这个盒子）
For each pair, calculate the \(t_{min}\) and \(t_{max}\) (negative is fine)
For the 3D box, \(t_{enter} = \max\{t_{min}\}, t_{exit} = \min\{t_{max}\}\)
If \(t_{enter} < t_{exit}\), we know the ray stays a while in the box (so they must intersect!)
physical correctness
- \(t_{exit}<0\), The box is "behind" the ray — no intersection
- \(t_{exit}\ge0, t_{enter}<0\), The ray’s origin is inside the box — certainly have intersection

In summary, Ray and AABB intersect iff

\[ t_{enter} < t_{exit}\ \text{and}\ t_{exit}\ge0 \]

Why Axis-Aligned¶

在求交时计算方便

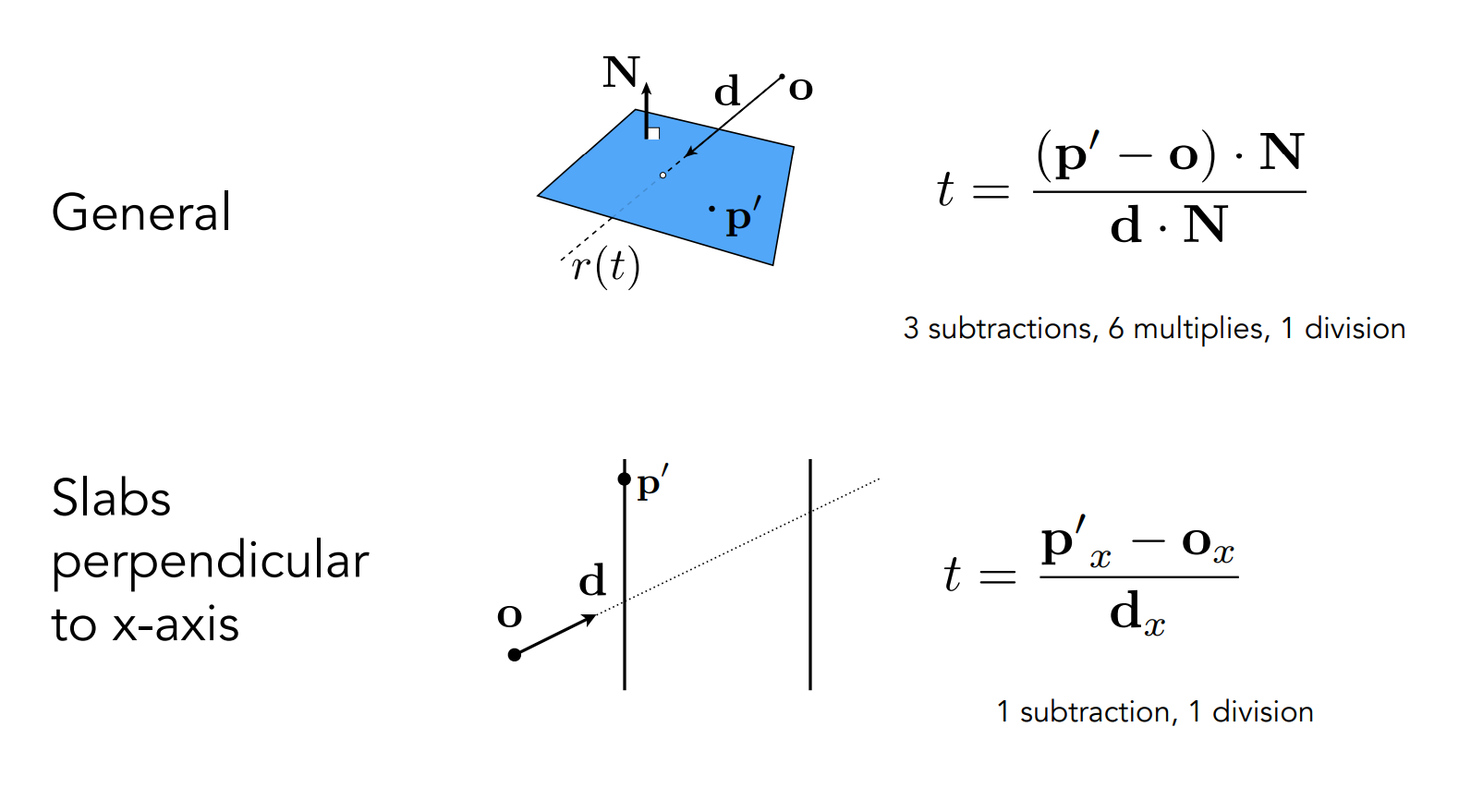
Using AABBs to accelerate ray tracing¶

Uniform Spatial Partitions (Grids)¶

Precomputation

Find bounding box
Create grid
Store each object in overlapping cells
- 只考虑物体的表面

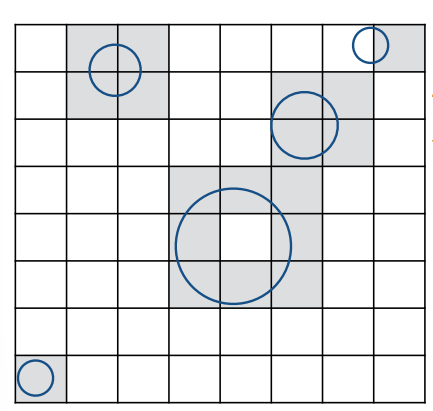
Ray Tracing

Step through grid in ray traversal order
For each grid cell, Test intersection with all objects stored at that cell
- 让光线经过各个包围盒中的区块，让光线和盒子求交（假设光线和盒子求交的运行速度远大于和物体求交的运行速度）
- 如果发现和光线相交的盒子内有物体，再让物体和盒子求交，通过这样找到所有的交点

Grid Resolution?
- Heuristic
- #cells = C * #objs
- C = 27 in 3D
Pros & Cons

Spatial Partitions¶

基于 Grid 方法的优化，物体稀疏的地方不需要用很多格子
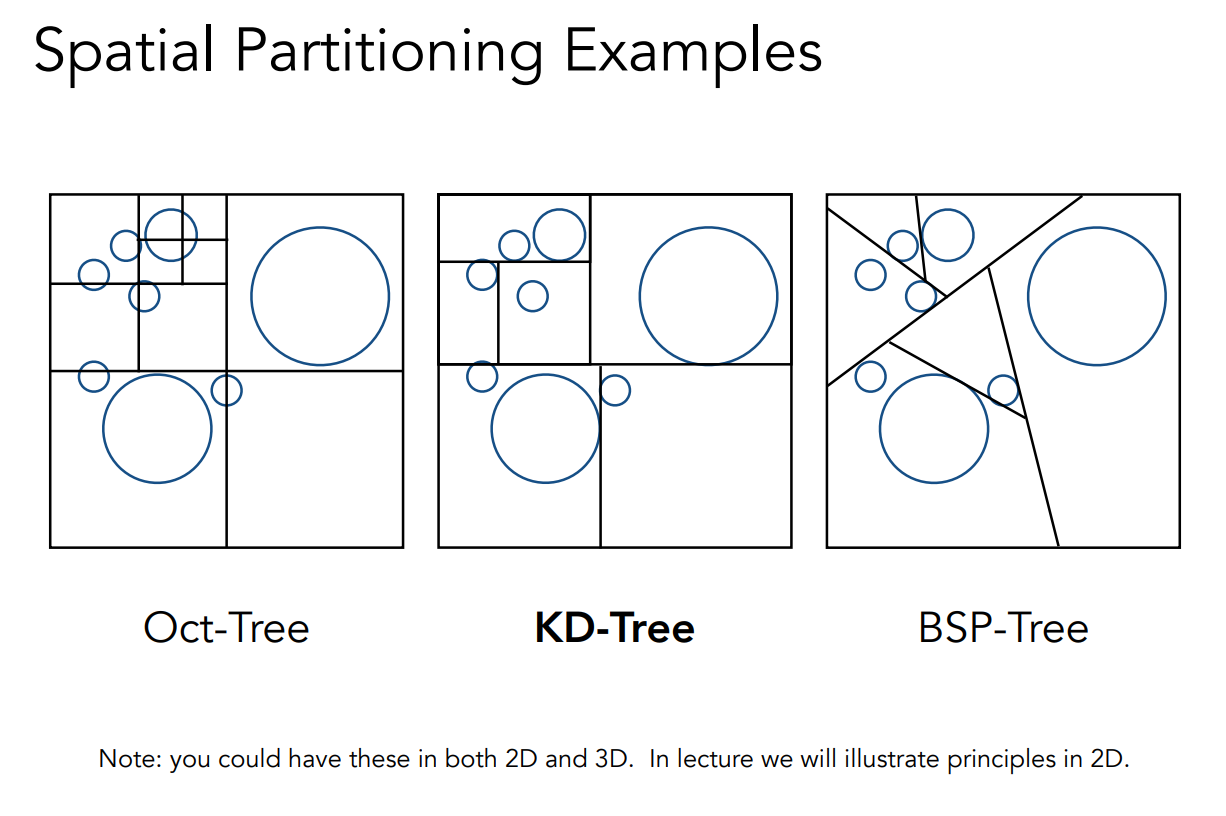
Examples
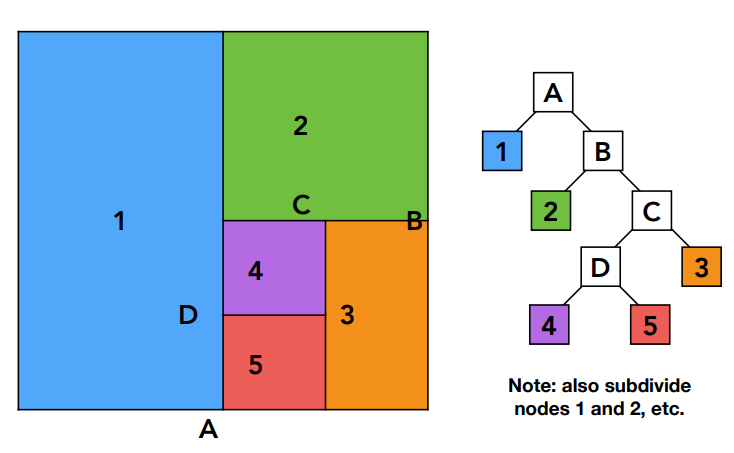
- Oct-Tree: 以下的八叉树是二维的情况，在二维空间中就是四叉的，把空间切成了不均匀的结构
- KD-Tree: KD-Tree 永远是找到一个轴把空间分成两个部分，和维数无关，把空间划分成了类似二叉树的结构，水平划分和数值划分是交替的以保证空间的划分是均匀的，计算简单
- BSP-Tree: 对空间的二分方法，每一次选择一个方向把节点的分开，和 KD-Tree 的区别是不是横平竖直的划分，会随着维度的升高计算变得复杂

KD-Tree Pre-Processing
- 此处只考虑每个格子划分了一次，实际中别的格子可能也需要划分
- 只在叶子节点存储三角形

Data Structure for KD-Trees
- Internal nodes store
- split axis: x-, y-, or z-axis
- split position: coordinate of split plane along axis
- children: pointers to child nodes
- No objects are stored in internal nodes
- Leaf nodes store
- list of objects
Cons of KD-Tree
- 很难判定一个三角形是否和一个立方体有交集，算法很难实现
- 如果一个物体和多个盒子都有交集（出现在多个叶子节点中），KD-Tree 在这点上并不直观

Object Partitions & Bounding Volume Hierarchy (BVH)¶

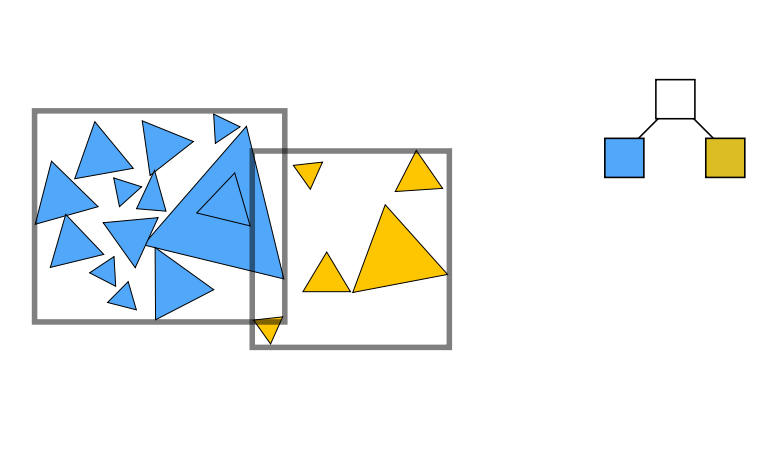
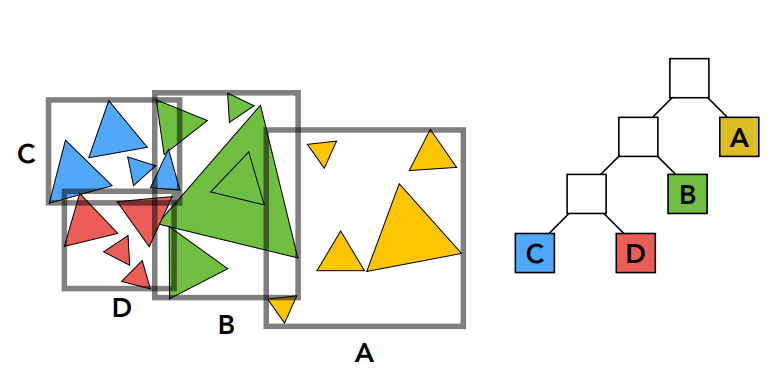
划分物体而不是划分空间
对于下图，把三角形划分成蓝色和黄色三角形，并重新计算蓝色和黄色三角形的包围盒
终止条件是一堆里最多有 \(N\) 个三角形

Pros of BVH
- 节省了三角形和包围盒求交问题
- 保证了一个三角形只在一个盒子里
Cons of BVH
- 不同的 Bounding Box 是有可能相交的
- 不能解决动态的物体，BVH 需要重新计算
Summary
- Find bounding box
- Recursively split set of objects in two subsets
- Recompute the bounding box of the subsets
- Stop when necessary
- Store objects in each leaf node
Methods to subdivide a node
- Choose a dimension to split
- Heuristic #1: Always choose the longest axis in node
- 让最长的轴变短，让最终的划分是比较均匀的
- Heuristic #2: Split node at location of median object
- 取中间的物体指的是，如果有 \(n\) 个三角形，找的是 \(\frac{n}{2}\) 处的三角形，保证切分后的三角形数量差不多，以保证生成的树是平衡的，减少最终的搜索时间
- 给任意一列无序的数，找到它第 \(i\) 大的数，可以使用快速选择算法，在 \(O(n)\) 内解决
Termination criteria
- Heuristic: stop when node contains few elements (e.g. 5)
Data Structure for BVHs
- Internal nodes store
- Bounding box
- Children: pointers to child nodes
- Leaf nodes store
- Bounding box
- List of objects
- Nodes represent subset of primitives in scene
- All objects in subtree

BVH Traversal¶

fun Intersect(Ray ray, BVH node) {
     if (ray misses node.bbox) return;

     if (node is a leaf node)
         test intersection with all objs;
         return closest intersection;

     hit1 = Intersect(ray, node.child1);
     hit2 = Intersect(ray, node.child2);

     return the closer of hit1, hit2;
}

Basic Radiometry¶

Chinese Name: 辐射度量学

Why Radiometry¶

在计算光强的时候，我们没有准确的物理定义
辐射度量学：定义了一系列方法和单位去描述光照
Accurately measure the spatial properties of light
- New terms: Radiant flux, intensity, irradiance, radiance
Perform lighting calculations in a physically correct manner

Light Measurements

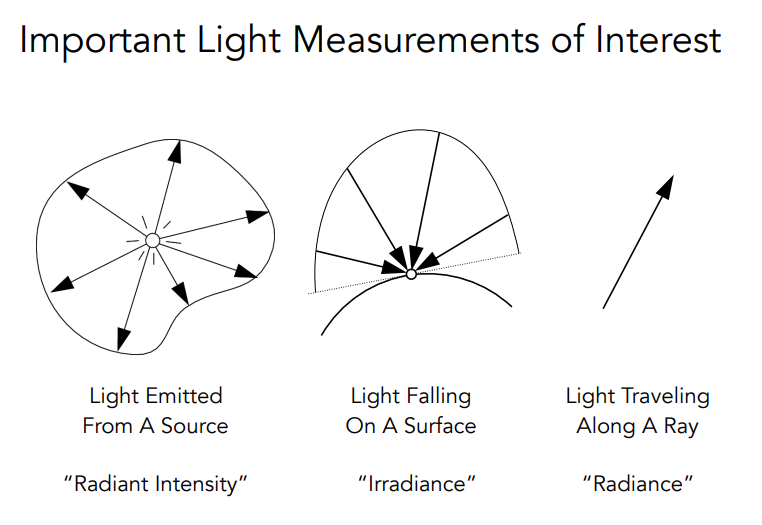
Radiant Energy and Flux (Power)¶

Radiant Energy: 光源辐射出来的能量 (Barely used in CG)

\[ Q[\mathrm{~J}=\text { Joule }] \]

Flux (Power): 光源辐射出的单位时间的能量，目的是分析和比较两个和多个能量（去除时间的影响）
- lm = lumen (Flux 的单位，翻译是流明)
- Flux 也可以理解为单位时间通过一个感光平面的光子数目

\[ \Phi \equiv \frac{\mathrm{d} Q}{\mathrm{~d} t}[\mathrm{~W}=\mathrm{Watt}][\operatorname{lm}=\text { lumen }]^* \]

Radiant Intensity¶

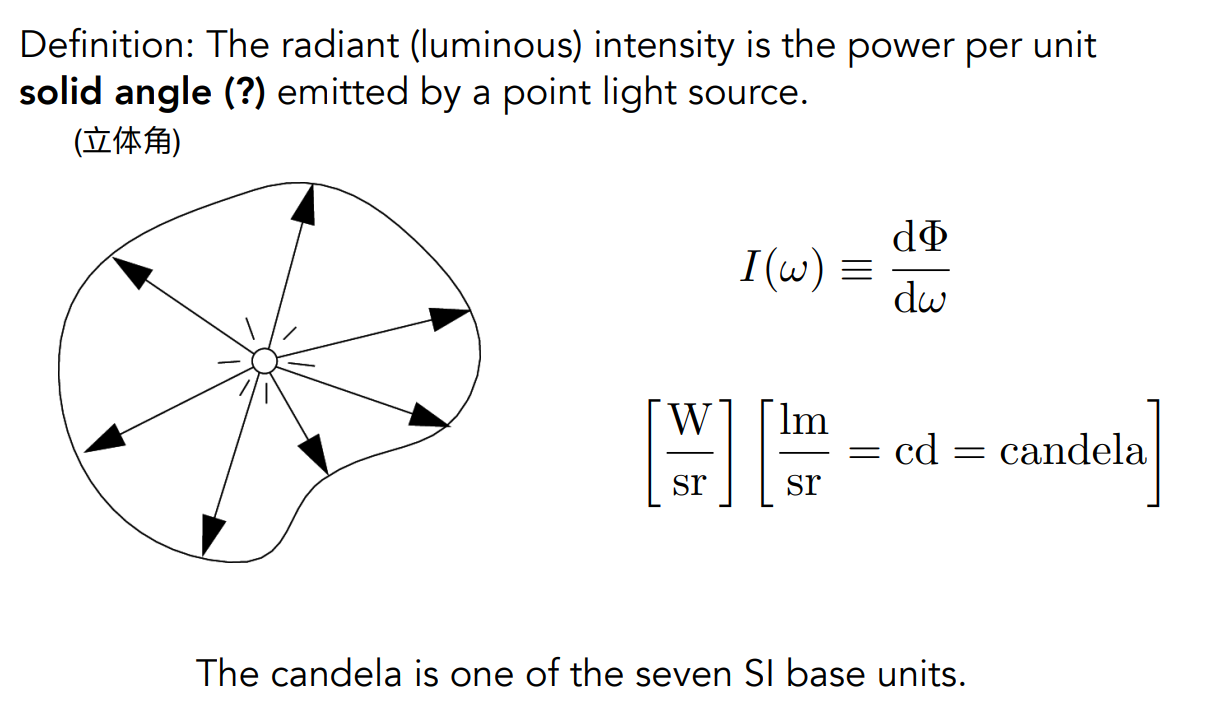
Radiant Intensity: The radiant (luminous) intensity is the power per unit solid angle (立体角) emitted by a point light source.
- 可以理解为能量除以立体角
- 定义了光源在任何一个方向上的亮度

\[ \begin{gathered} I(\omega) \equiv \frac{\mathrm{d} \Phi}{\mathrm{d} \omega} \\ {\left[\frac{\mathrm{W}}{\mathrm{sr}}\right]\left[\frac{\operatorname{lm}}{\mathrm{sr}}=\mathrm{cd}=\text { candela }\right]} \end{gathered} \]

Angles and Solid Angles¶

Angle: ratio of subtended arc length on circle to radius
- \(\theta=\frac{l}{r}\)
- Circle has \(2 \pi\) radians
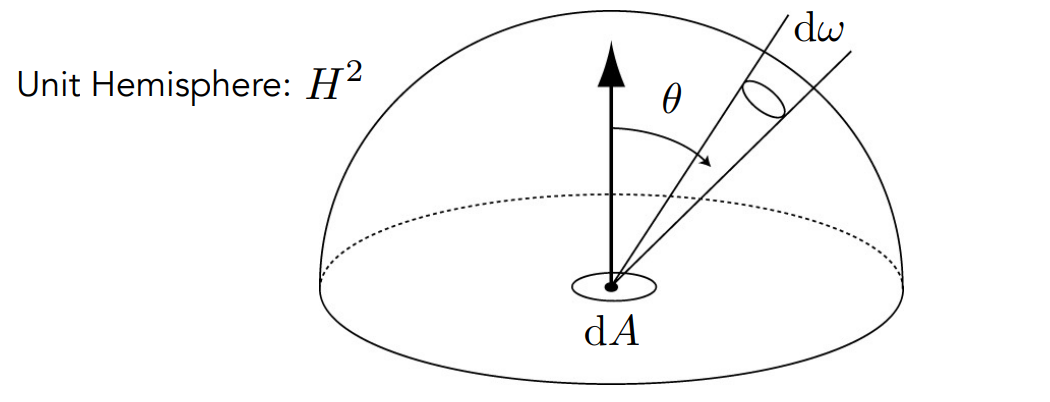
Solid angle: ratio of subtended area on sphere to radius squared
- 弧度制在三维空间中的延申，在三维空间中找一个球，从球出发形成某个大小的锥，锥会打到球面上，形成一个面积 \(A\)，立体角是它除以半径的平方
- 把任何一个物体投影到单位球上，在单位球上框出的范围就是立体角
- 描述一个空间中角有多大
- \(\Omega=\frac{A}{r^2}\)
- Sphere has \(4 \pi\) steradians(立体角的单位)

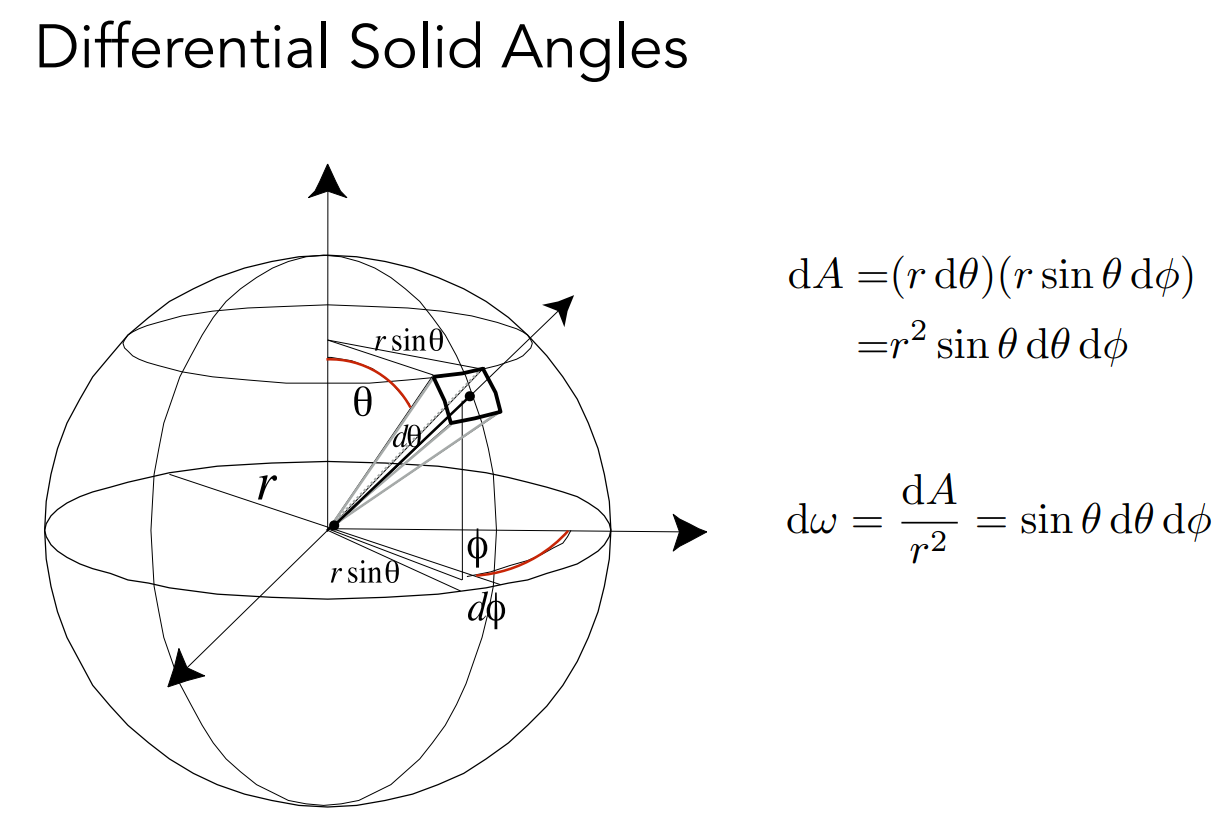
Differential Solid Angles¶

Differential Solid Angles: 微分立体角
通常使用 \(\omega\) 来定义单位方向

Isotropic Point Source¶

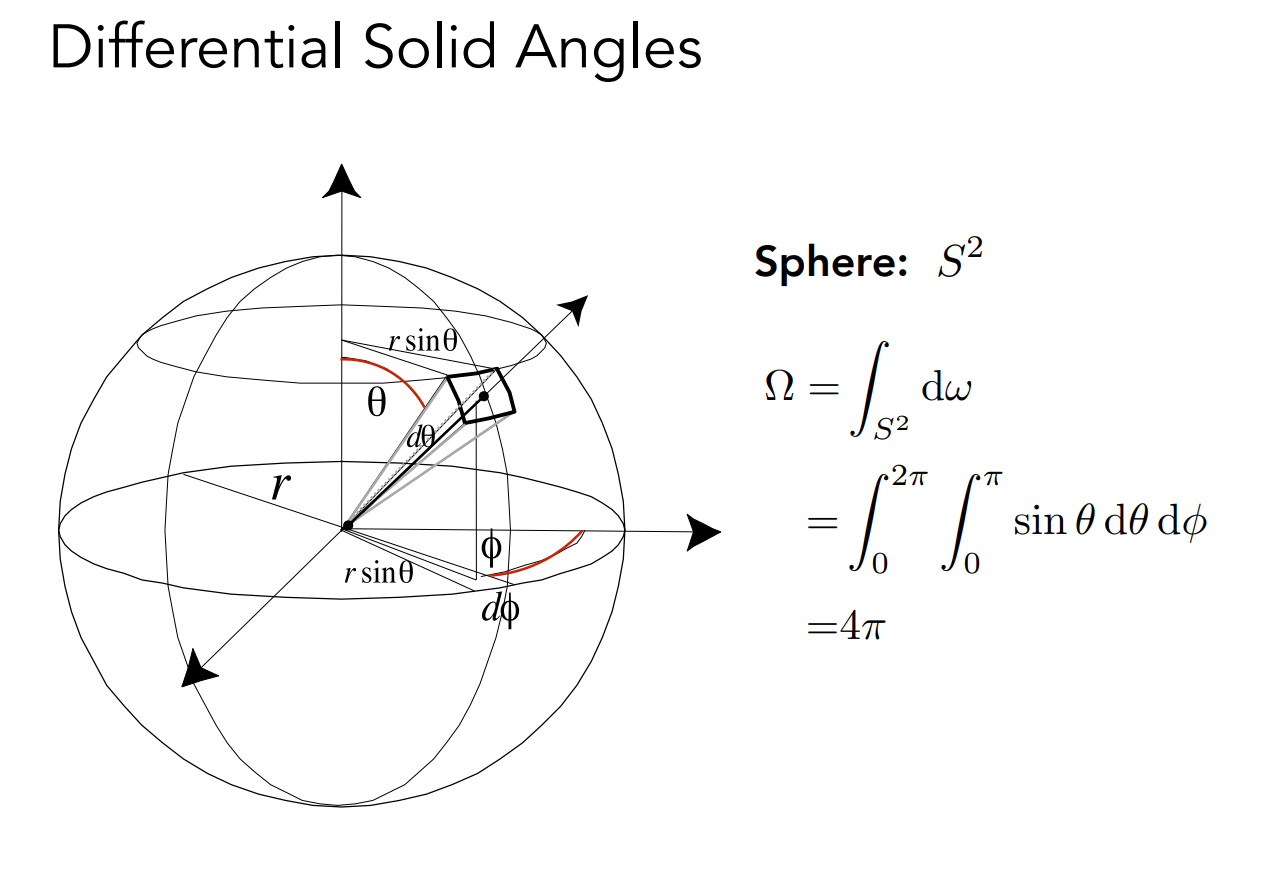
对于一个均匀点光源，它的 Radiant Intensity 的相关计算是
- 对于所有方向上的 Intensity 积分起来可以得到 Flux
\[ \begin{aligned} \Phi &=\int_{S^2} I \mathrm{~d} \omega \\ &=4 \pi I \end{aligned} \]
- 对于任何一个方向上的 Intensity 有

\(\( I=\frac{\Phi}{4 \pi} \)\)

Irradiance¶

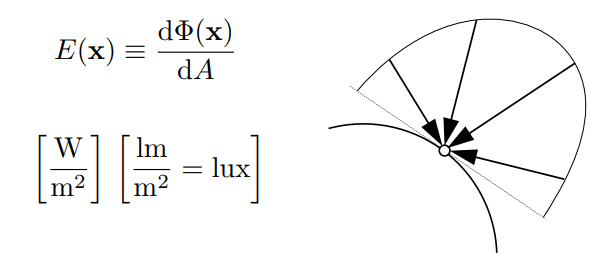
The irradiance is the power per unit area incident on a surface point.
- Intensity: power per soild angle
- 注意，面需要和入射光线垂直

\[ \begin{gathered} E(\mathbf{x}) \equiv \frac{\mathrm{d} \Phi(\mathbf{x})}{\mathrm{d} A} \\ {\left[\frac{\mathrm{W}}{\mathrm{m}^2}\right]\left[\frac{\operatorname{lm}}{\mathrm{m}^2}=\operatorname{lux}\right]} \end{gathered} \]

Radiance¶

Radiance is the fundamental field quantity that describes the distribution of light in an environment

Radiance: The radiance (luminance) is the power emitted, reflected, transmitted or received by a surface, per unit solid angle, per projected unit area.
- 考虑某一个确定的微小面和一个方向

\[ L(\mathrm{p}, \omega) \equiv \frac{\mathrm{d}^2 \Phi(\mathrm{p}, \omega)}{\mathrm{d} \omega \mathrm{d} A \cos \theta} \]

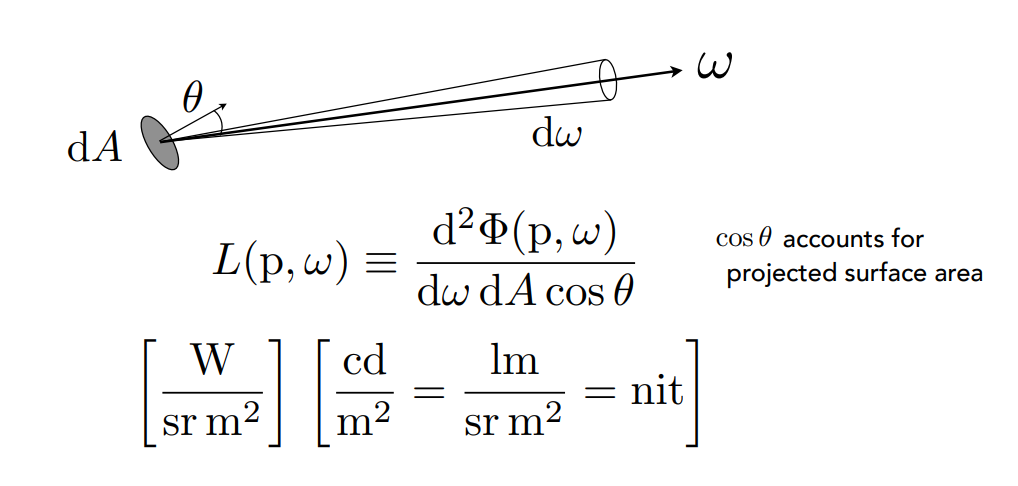
Recall
- Irradiance: power per projected unit area
- Intensity: power per solid angle
So
- Radiance: Irradiance per solid angle
- Radiance: Intensity per projected unit area

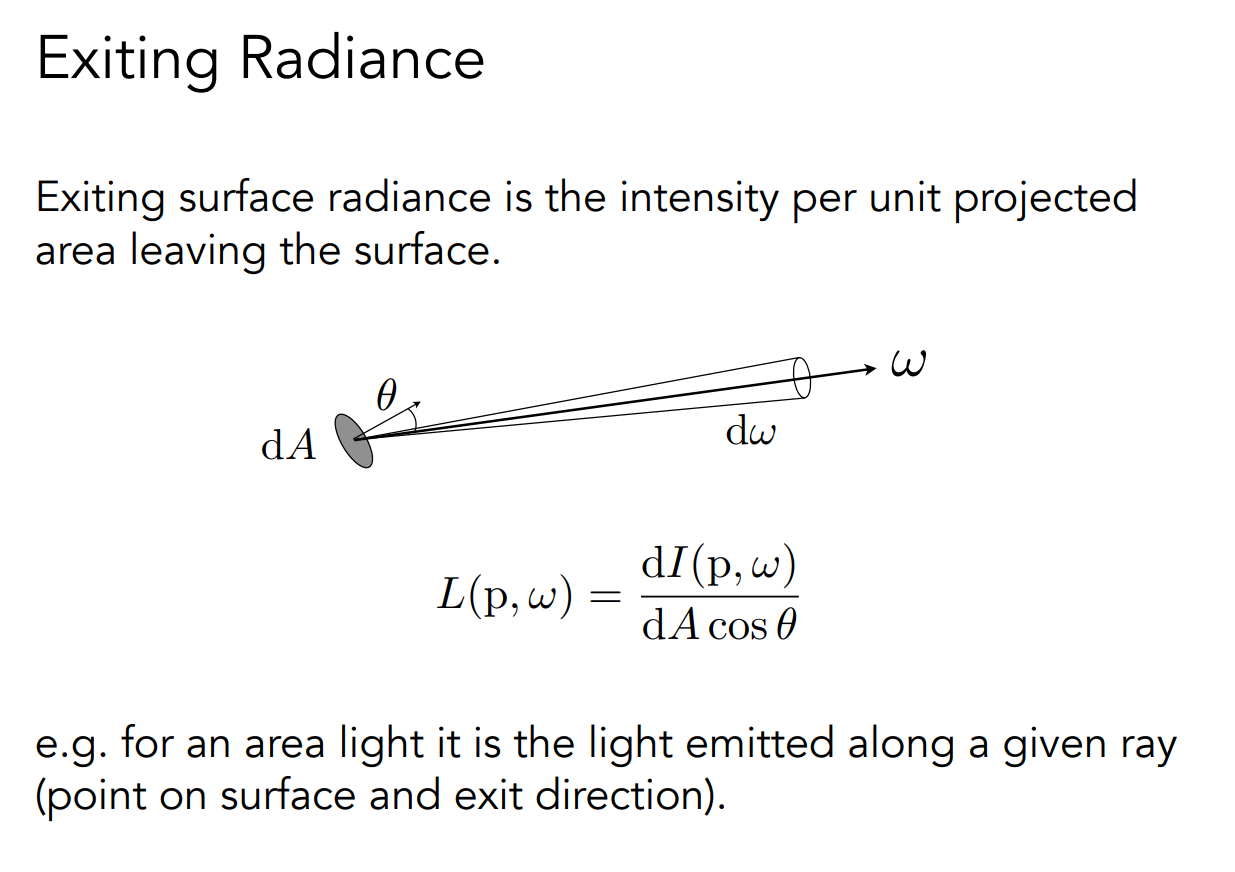
Irradiance vs. Radiance¶

Irradiance: total power received by area dA
- 某一个小区域内接收到的所以能量
Radiance: power received by area dA from “direction” dω
- 某一个小区域的某一个方向上接受到的能量

\[ \begin{aligned} d E(\mathrm{p}, \omega) &=L_i(\mathrm{p}, \omega) \cos \theta \mathrm{d} \omega \\ E(\mathrm{p}) &=\int_{H^2} L_i(\mathrm{p}, \omega) \cos \theta \mathrm{d} \omega \end{aligned} \]

Bidirectional Reflectance Distribution Function (BRDF)¶

双向反射分布函数
告诉你不同反射方向上分布的能量情况

Reflection at a Point¶

Radiance from direction ωi turns into the power E that dA receives Then power E will become the radiance to any other direction ωo

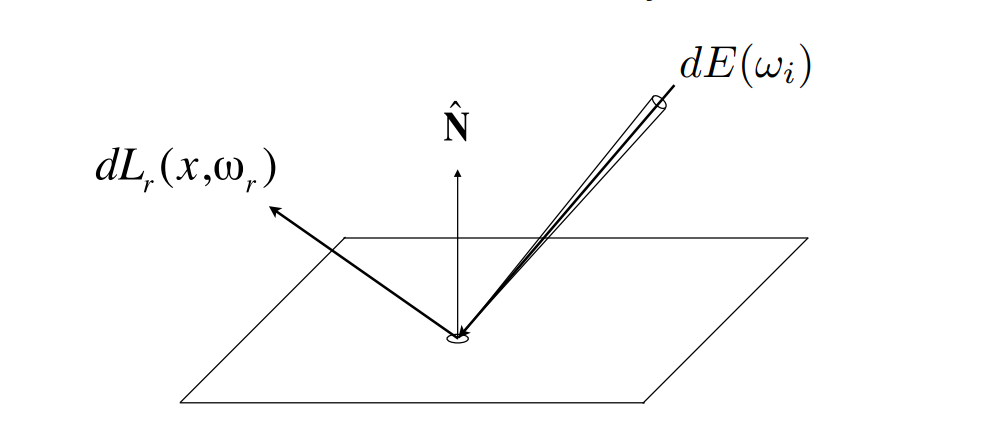
Differential irradiance incoming: \(\quad d E\left(\omega_i\right)=L\left(\omega_i\right) \cos \theta_i d \omega_i\)
Differential radiance exiting (due to \(d E\left(\omega_i\right)\) ): \(\quad d L_r\left(\omega_r\right)\)

BRDF¶

The Bidirectional Reflectance Distribution Function (BRDF) represents how much light is reflected into each outgoing direction \(\omega_r\) from each incoming direction

BRDF 描述了光线和物体是如何作用的

\[ f_r\left(\omega_i \rightarrow \omega_r\right)=\frac{\mathrm{d} L_r\left(\omega_r\right)}{\mathrm{d} E_i\left(\omega_i\right)}=\frac{\mathrm{d} L_r\left(\omega_r\right)}{L_i\left(\omega_i\right) \cos \theta_i \mathrm{~d} \omega_i} \quad\left[\frac{1}{\mathrm{sr}}\right] \]

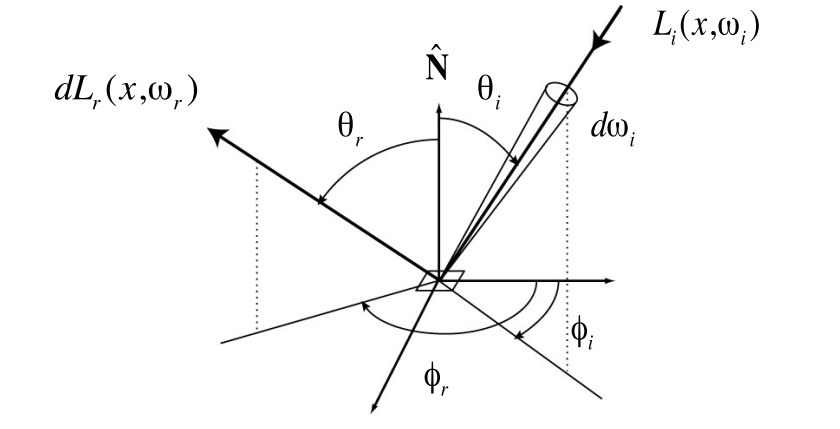
The Reflection Equation¶

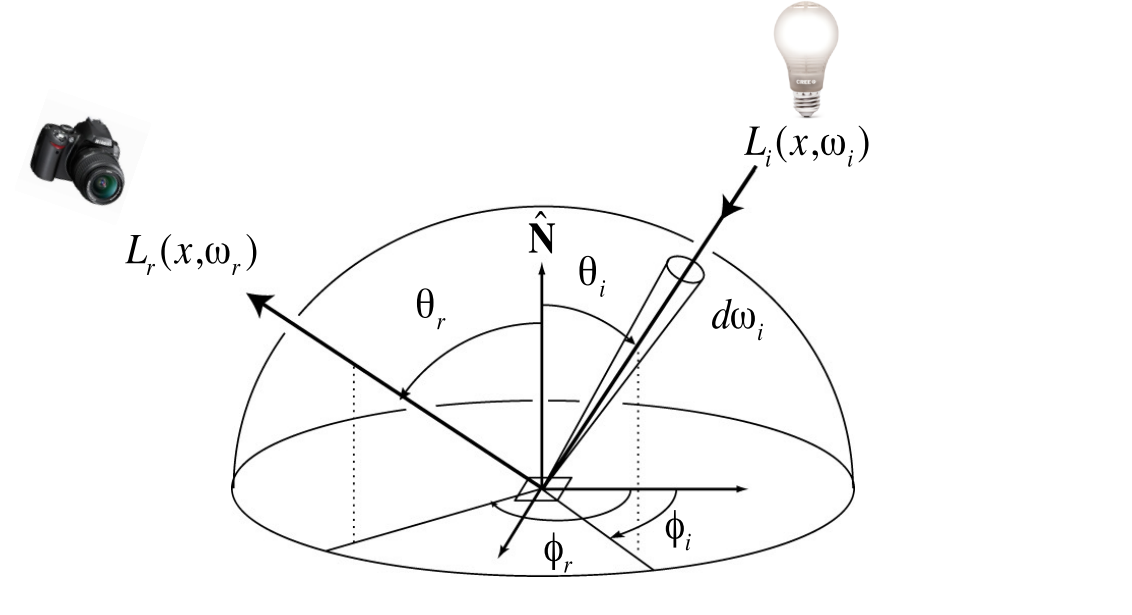
Reflection Equation 描述了任何一个着色点在各种不同光照环境下对出射光线的贡献

\[ L_r\left(\mathrm{p}, \omega_r\right)=\int_{H^2} f_r\left(\mathrm{p}, \omega_i \rightarrow \omega_r\right) L_i\left(\mathrm{p}, \omega_i\right) \cos \theta_i \mathrm{~d} \omega_i \]

Challenge: Recursive Equation¶

能够到达着色点的光线不止有光源，还有其他物体的反射出去的 Radiance

The Rendering Equation¶

Re-write the reflection equation:

\[ L_r\left(\mathrm{p}, \omega_r\right)=\int_{H^2} f_r\left(\mathrm{p}, \omega_i \rightarrow \omega_r\right) L_i\left(\mathrm{p}, \omega_i\right) \cos \theta_i \mathrm{~d} \omega_i \]

by adding an Emission term to make it general（考虑物体会发光的情况），这样就得到了 Rendering Equation

\[ L_o\left(p, \omega_o\right)=L_e\left(p, \omega_o\right)+\int_{\Omega^{+}} L_i\left(p, \omega_i\right) f_r\left(p, \omega_i, \omega_o\right)\left(n \cdot \omega_i\right) \mathrm{d} \omega_i \]

Note: now, we assume that all directions are pointing outwards!

Understanding the rendering equation¶

Reflection Equation¶

当有一个点光源时

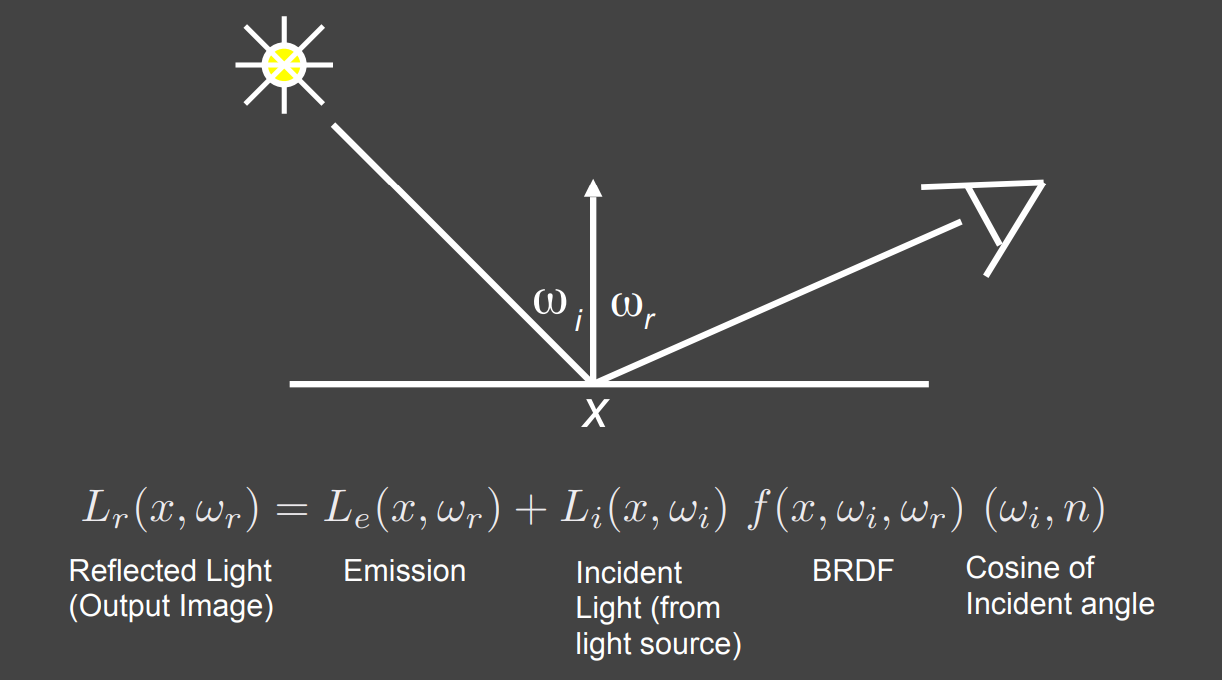
当有很多点光源时

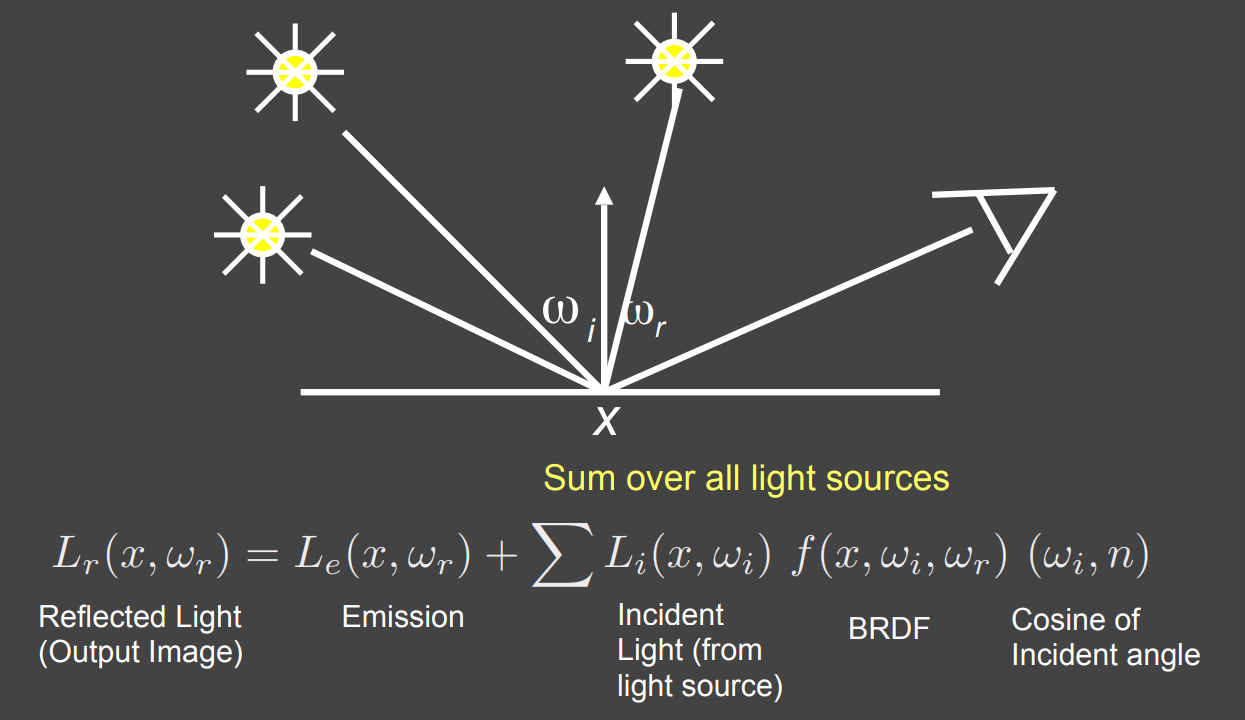
当有面光源时（看成点光源的集合）

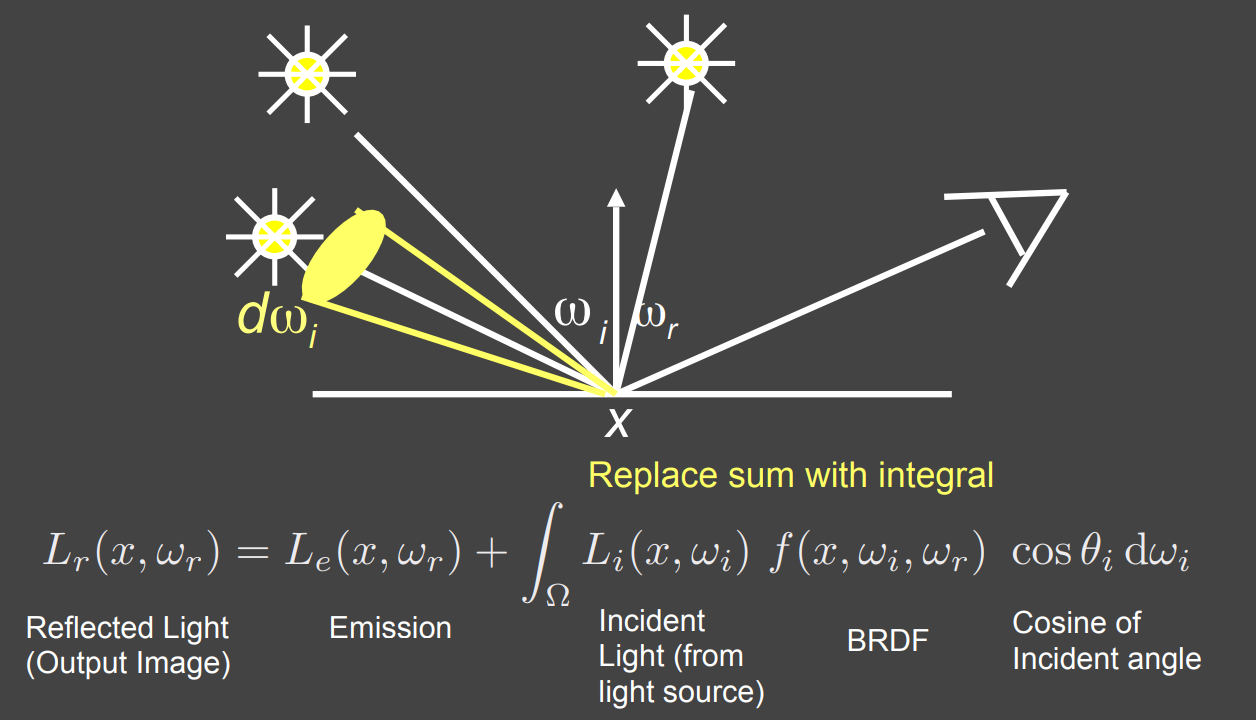
当有其他物体反射的 Radiance 时

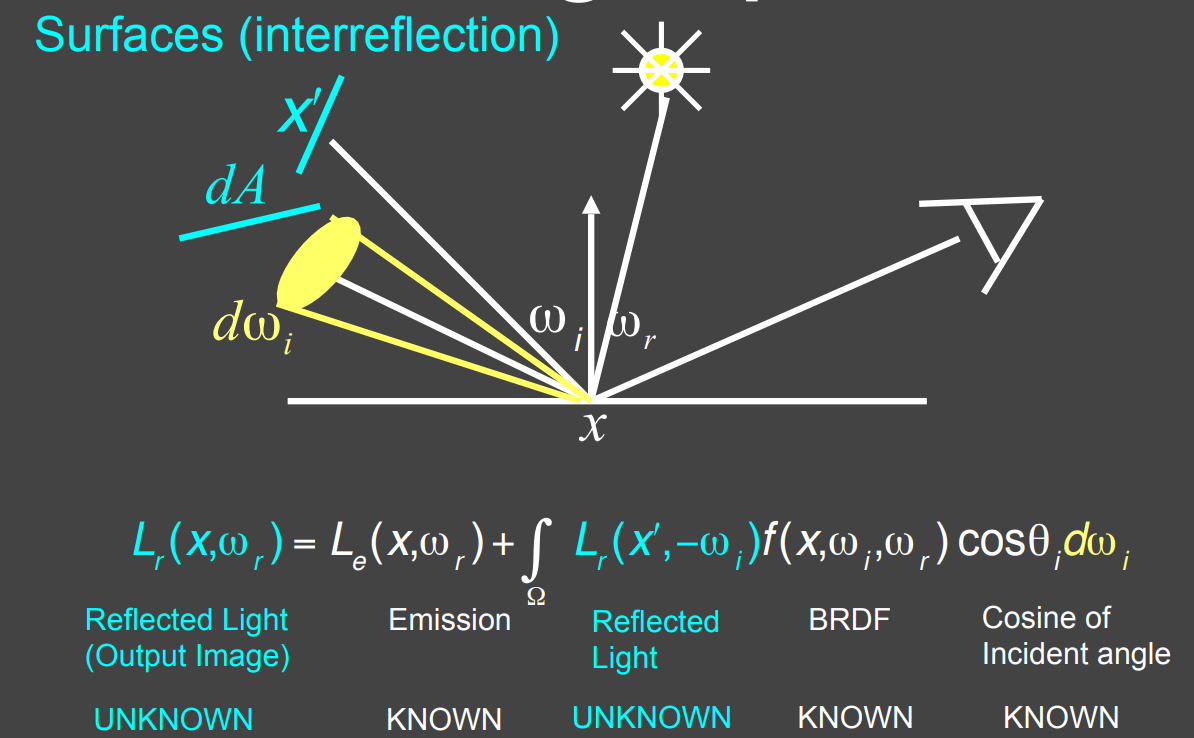
Rendering Equation as Integral Equation¶

对渲染方程进行简写后的结果

Linear Operator Equation¶

简化写成算子形式，目的是对渲染方程进行求解，中间省略了很多步骤

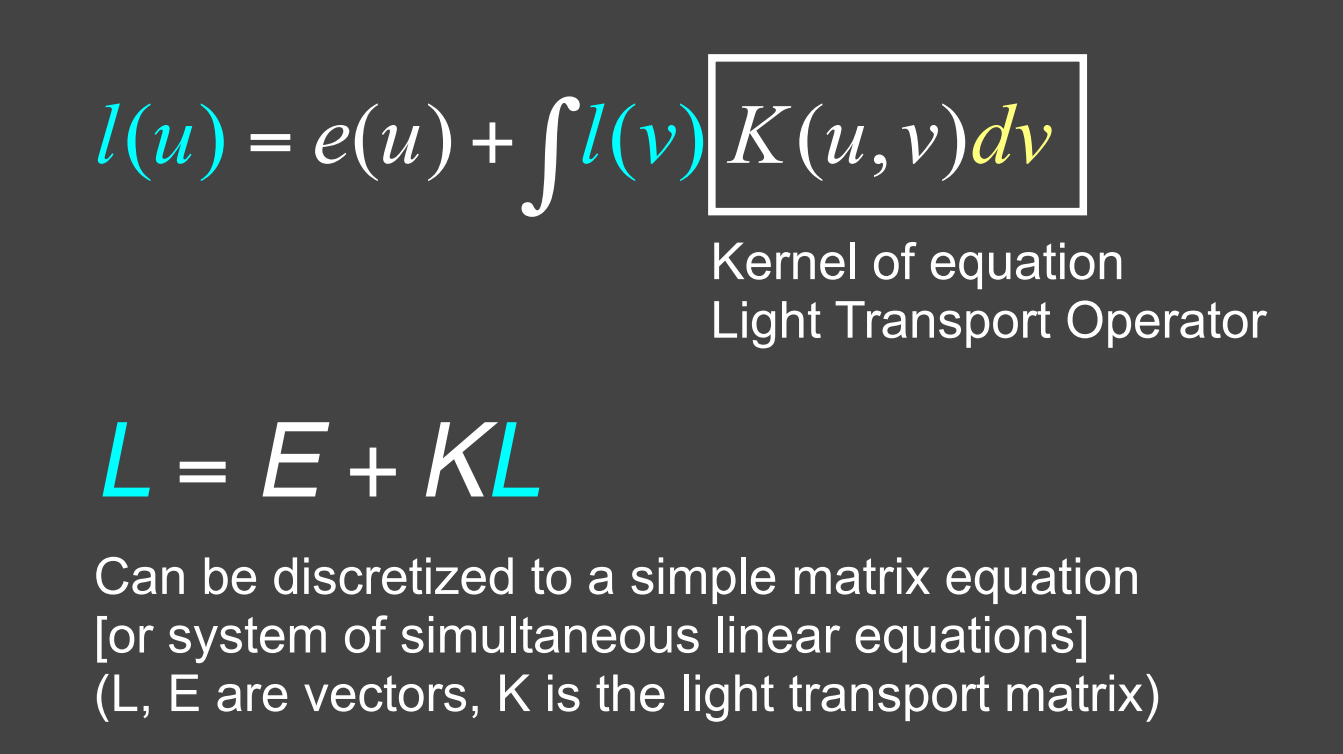
Ray Tracing and extensions¶

General class numerical Monte Carlo methods
Approximate set of all paths of light in scene

Ray Tracing¶

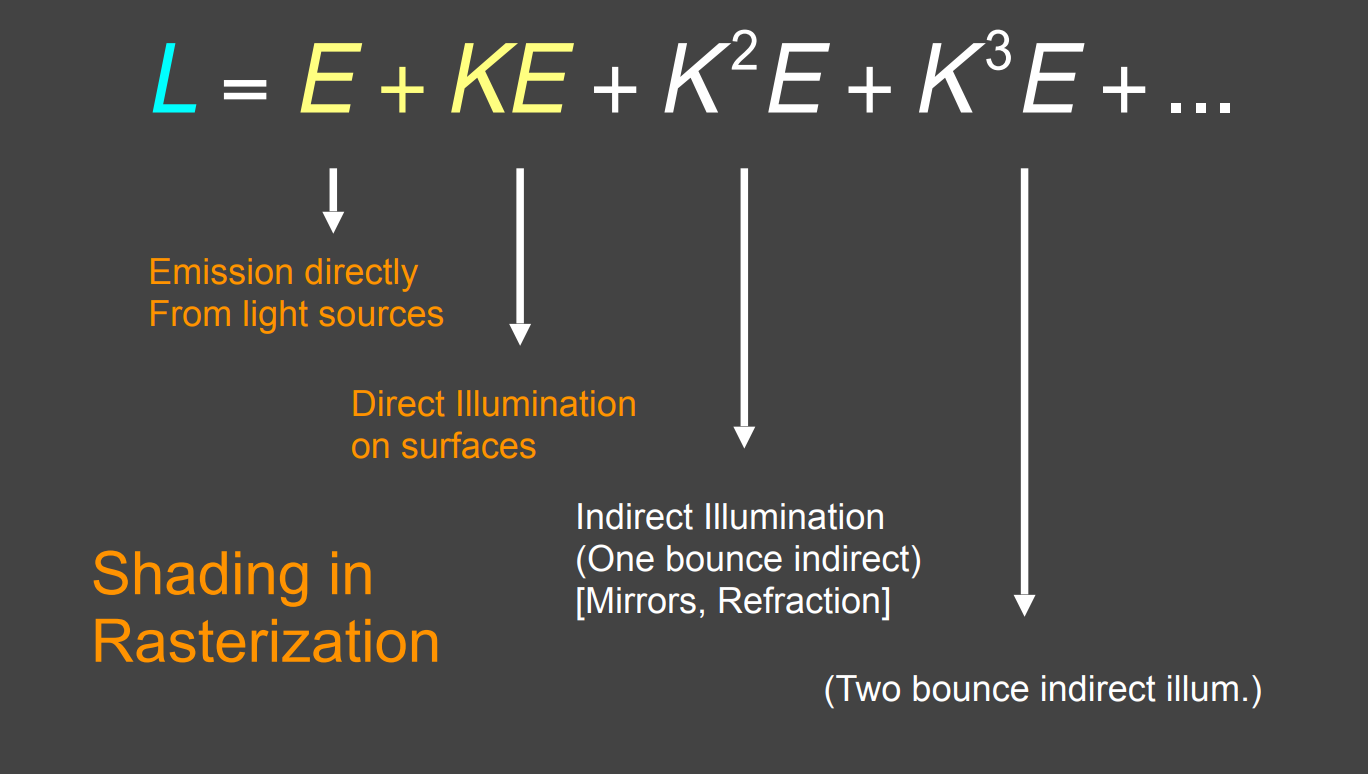
将最后看到的图写成直接看到光源、弹射一次、弹射二次....、弹射 \(n\) 次的和，结果是全局光照

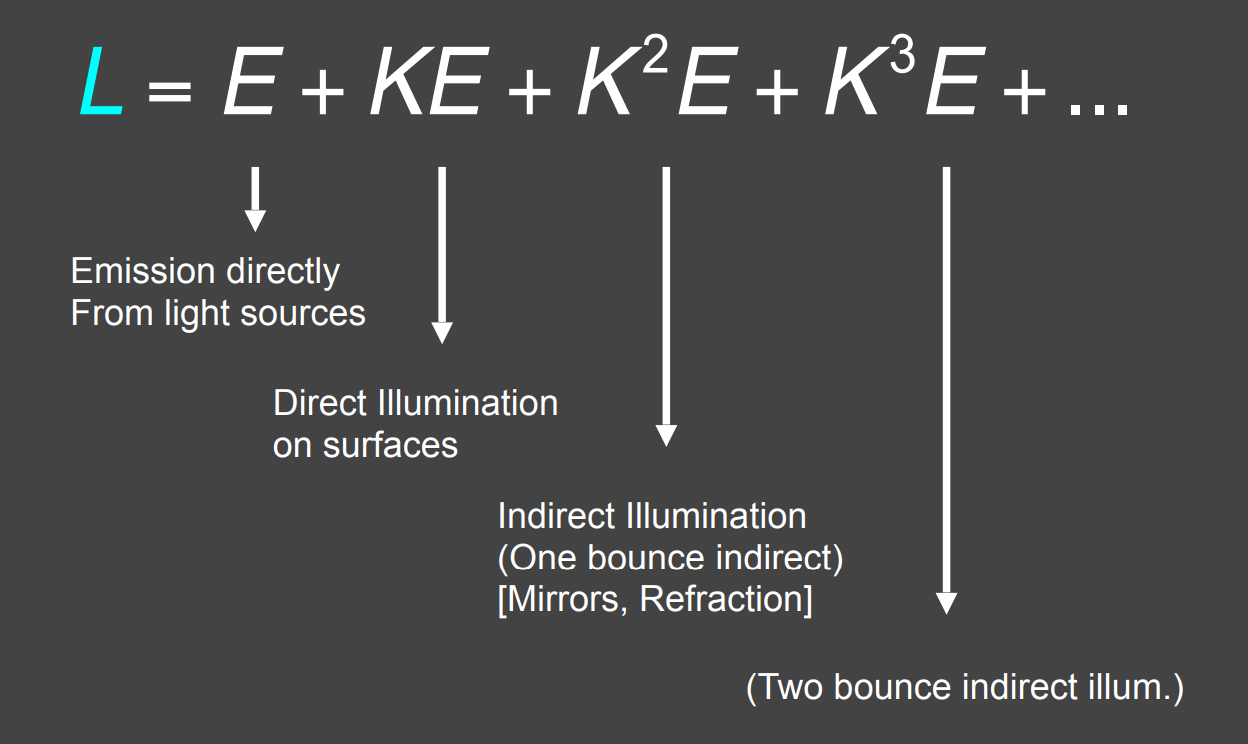
光栅化只解决了 \(E+KE\) 部分

Monte Carlo Path Tracing¶

Monte Carlo Integration¶

Why&What Monte Carlo Integration¶

对于给定函数的定积分，直接通过解析计算求解难度太大
Monte Carlo Integration 是一种数值方法，求出的只是一个数
在积分域内不断采样，假设积分区域是长方形，对于所有采样得到的结果求平均

Define Monte Carlo Integration¶

Definite integral

\[ \quad \int_a^b f(x) d x \]

Random variable

\[ \quad X_i \sim p(x) \]

Monte Carlo estimator

\[ \quad F_N=\int f(x) \mathrm{d} x=\frac{1}{N} \sum_{i=1}^N \frac{f\left(X_i\right)}{p\left(X_i\right)} \]

Note that
- The more samples, the less variance.
- Sample on \(x\), integrate on \(x\).

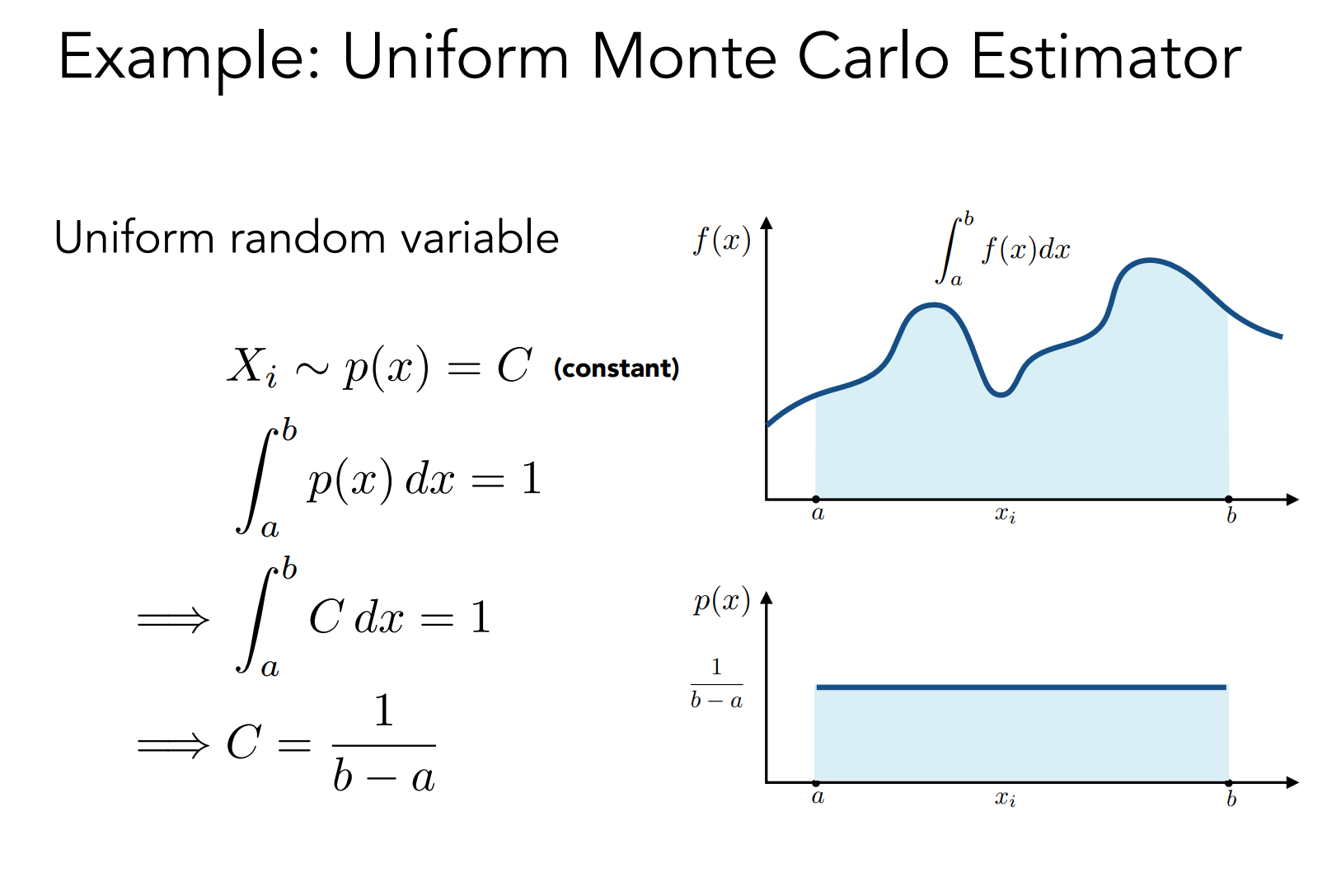
如果随机变量均匀采样（均匀分布），Monte Carlo Integration 有以下形式
- Definite integral
\[ \int_a^b f(x) d x \]
- Uniform random variable

\(\( X_i \sim p(x)=\frac{1}{b-a} \)\)

- Basic Monte Carlo estimator

\(\( F_N=\frac{b-a}{N} \sum_{i=1}^N f\left(X_i\right) \)\)

Path Tracing¶

Motivation: Problems of Whitted-Style Ray Tracing¶

For Whitted-style ray tracing, it has some cons/ simplifications

Always perform specular reflections / refractions
Stop bouncing at diffuse surfaces

Whitted-Style Ray Tracing: Problem 1¶

Whitted-Style Ray Tracing 对于 glossy materials 还认为光线是镜面反射的话是不对的

Whitted-Style Ray Tracing: Problem 2¶

对于 Whitted-Style Ray Tracing, No reflections between diffuse materials
- 体现在接触不到光的漫反射面反射出了接触到光的红色面的光 (color bleeding)

Problem Summary: Whitted-Style Ray Tracing is Wrong¶

But the rendering equation is correct

\[ L_o\left(p, \omega_o\right)=L_e\left(p, \omega_o\right)+\int_{\Omega^{+}} L_i\left(p, \omega_i\right) f_r\left(p, \omega_i, \omega_o\right)\left(n \cdot \omega_i\right) \mathrm{d} \omega_i \]

But it involves

Solving an integral over the hemisphere, and
Recursive execution

A Simple Monte Carlo Solution¶

因此，对于着色点 \(p\) 的 Monte Carlo Integration 为

\[ \begin{aligned} L_o\left(p, \omega_o\right) &=\int_{\Omega^{+}} L_i\left(p, \omega_i\right) f_r\left(p, \omega_i, \omega_o\right)\left(n \cdot \omega_i\right) \mathrm{d} \omega_i \\ & \approx \frac{1}{N} \sum_{i=1}^N \frac{L_i\left(p, \omega_i\right) f_r\left(p, \omega_i, \omega_o\right)\left(n \cdot \omega_i\right)}{p\left(\omega_i\right)} \end{aligned} \]

shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
    Return Lo

Introducing Global Illumination¶

Naive Algorithm¶

考虑物体反射过来的光线，如果打到物体，就递归计算

shade(p, wo)
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi
        Trace a ray r(p, wi)
        If ray r hit the light  
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        Else If ray r hit an object at q
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi)
    Return Lo

Problem #1: Explosion of #rays as #bounces go up - let N = 1!¶

光线仅仅弹射两次的话数量级就已经不可以接受了
Key observation: #rays will not explode iff \(N = 1\)
- 当使用 \(N = 1\) 进行 Monte Carlo Integration 时 \(\to\) 路径追踪 (path tracing)
- 当使用 \(N \ne 1\) 进行 Monte Carlo Integration 时 \(\to\) 分布式光线追踪
使用 \(N = 1\) 进行 Monte Carlo Integration 噪声很大，但只要使用多个路径穿过一个像素对它们求平均即可

修改刚刚的算法

shade(p, wo)
    Randomly choose ONE direction wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light
        Return L_i * f_r * cosine / pdf(wi)
    Else If ray r hit an object at q
        Return shade(q, -wi) * f_r * cosine / pdf(wi)

ray_generation(camPos, pixel)
    Uniformly choose N sample positions within the pixel
    pixel_radiance = 0.0
    For each sample in the pixel
        Shoot a ray r(camPos, cam_to_sample)
        If ray r hit the scene at p
            pixel_radiance += 1 / N * shade(p, sample_to_cam)
    Return pixel_radiance

Problem #2: The recursive algorithm will never stop - Russian Roulette!¶

但是在真实世界中，光线是不会停止弹射的，限制弹射次数并不合理，因为对于弹射次数的削减相当于直接削减了能量，这违背了能量守恒定律
Solution: Russian Roulette (RR) （俄罗斯轮盘赌）
- 在一定的概率下停止追踪，方法如下 1. 假设得到的理想追踪结果为 \(L_o\) 2. 人工设定一个概率 \(P\ (0 < P < 1)\) 3. 以概率 \(P\) shoot a ray，返回 the shading result divided by \(P: L_o/ P\) 4. 以概率 \(1-P\) shoot a ray，返回 the shading result is \(0\)
- 在这种情况下的期望 \(E= P \times (L_o / P) + (1 - P) \times 0 = L_o\)

代码如下

shade(p, wo)
    Manually specify a probability P_RR
    Randomly select ksi in a uniform dist. in [0, 1]
    If (ksi > P_RR) return 0.0;

    Randomly choose ONE direction wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light
        Return L_i * f_r * cosine / pdf(wi) / P_RR
    Else If ray r hit an object at q
        Return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR

Problems of Path Tracing¶

Problem #1: Not very efficient¶

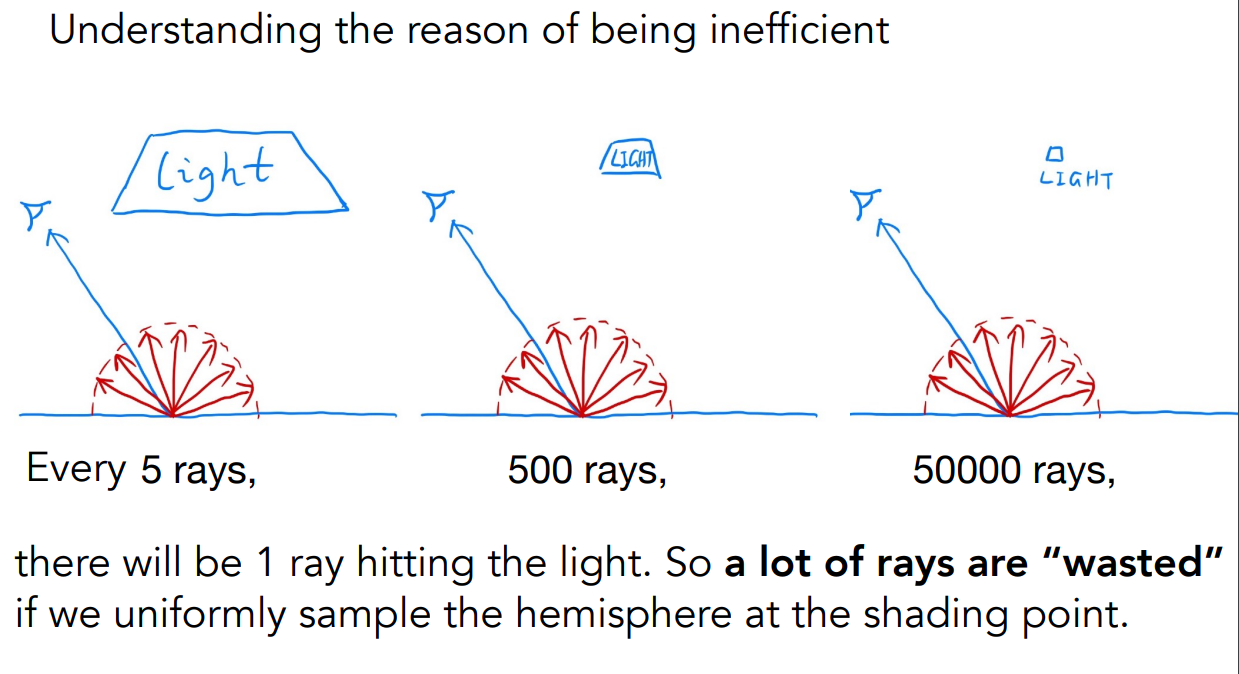
浪费现象产生的原因是我们均匀的在半球上采样，很大一部分采样没有进入光源，如果找到一个好的概率密度函数，可以提高效率 \(\to\) 直接在光源上进行采样

Solution #1: Sampling the Light (pure math)¶

Assume uniformly sampling on the light: \(\text{pdf} = 1 / A\) (because \(\int \text{pdf} \ \mathrm{d}A = 1\))
But the rendering equation integrates on the solid angle: \(L_o = \int L_i fr cos \ \mathrm{d} \omega.\)
- Recall Monte Carlo Integration: Sample on \(x\) & integrate on \(x\)
- we sample on the light, so we must integrate on the light
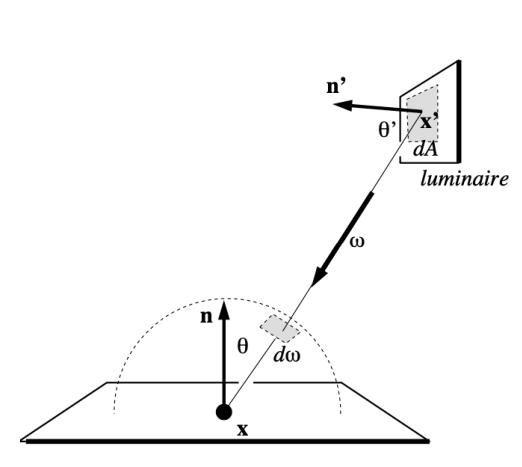
- 我们只要知道 \(\mathrm{d} \omega\) 和 \(\mathrm{d}A\) 的关系即可
- Recall the alternative def. of solid angle: Projected area on the unit sphere
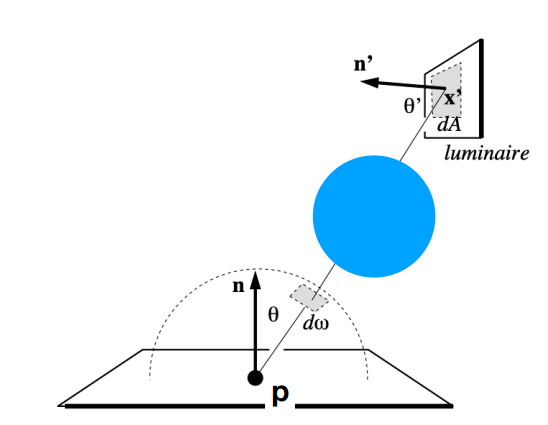
- 将 \(\mathrm{d}A\) 往单位球上投影即可 ( \(\mathrm{d} A \cos \theta^{\prime}\) 就是把面转到朝向中心的方向，根据立体角的定义来理解下面的式子)
\[ \mathrm{d} \omega=\frac{\mathrm{d} A \cos \theta^{\prime}}{\left\|x^{\prime}-x\right\|^2} \]
我们重写渲染方程即可（变量替换，改变积分域）

\(\( \begin{aligned} L_o\left(x, \omega_o\right) &=\int_{\Omega^{+}} L_i\left(x, \omega_i\right) f_r\left(x, \omega_i, \omega_o\right) \cos \theta \mathrm{d} \omega_i \\ &=\int_A L_i\left(x, \omega_i\right) f_r\left(x, \omega_i, \omega_o\right) \frac{\cos \theta \cos \theta^{\prime}}{\left\|x^{\prime}-x\right\|^2} \mathrm{~d} A \end{aligned} \)\)

Previously, we assume the light is “accidentally” shot by uniform hemisphere sampling

Now we consider the radiance coming from two parts:

light source (colored blue, direct, no need to have RR)
other reflectors (colored orange, indirect, RR)

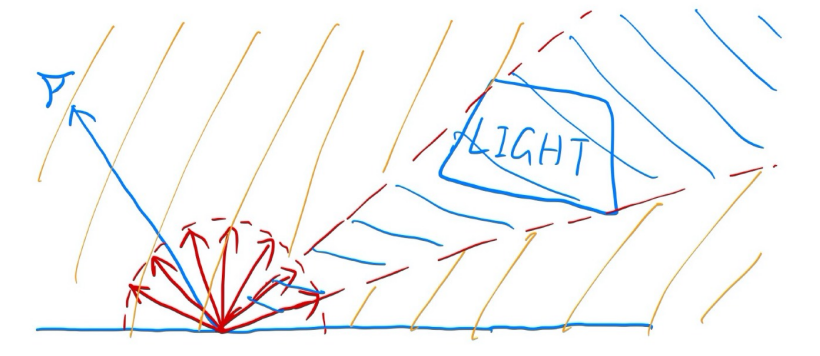
代码如下（拆分直接光照和间接光照）

shade(p, wo)
    # Contribution from the light source.
    Uniformly sample the light at x’ (pdf_light = 1 / A)
    L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light

    # Contribution from other reflectors.
    L_indir = 0.0
    Test Russian Roulette with probability P_RR
    Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)
    Trace a ray r(p, wi)
    If ray r hit a non-emitting object at q
        L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR

    Return L_dir + L_indir

Problem #2: Light is not blocked or not¶

在之前的计算中，假设了光线不会被挡到

Solution #2: Give a ray from P¶

考虑点 \(p\) 到 \(x'\) 的连线，从 \(p\) 点打一根光线，看看有没有被挡到

# Contribution from the light source.
L_dir = 0.0
Uniformly sample the light at x’ (pdf_light = 1 / A)
Shoot a ray from p to x’
If the ray is not blocked in the middle
    L_dir = …

Some Side Notes¶

Previous
- Ray tracing == Whitted-style ray tracing
Modern (my own definition)
- The general solution of light transport, including
- (Unidirectional & bidirectional) path tracing
- Photon mapping
- Metropolis light transport - VCM / UPBP…
Uniformly sampling the hemisphere
- How? And in general, how to sample any function? (sampling)
Monte Carlo integration allows arbitrary pdfs
- What's the best choice? (importance sampling)
- 重要性采样：针对某一种特定形状进行采样
Do random numbers matter?
- Yes! (low discrepancy sequences)
I can sample the hemisphere and the light
- Can I combine them? Yes! (multiple imp. sampling)
- 结合从半球和光源的采样方法
The radiance of a pixel is the average of radiance on all paths passing through it
- Why? (pixel reconstruction filter)
Is the radiance of a pixel the color of a pixel?
- No. (gamma correction, curves, color space)

Importance Sampling¶

让 PDF 正比于部分的被积函数

https://zhuanlan.zhihu.com/p/360420413

Last update: July 30, 2023
Created: June 16, 2023