Lecture 11-12 Geometry 2 (Curves and Surfaces)¶
Curves¶
Bézier Curves 贝塞尔曲线¶
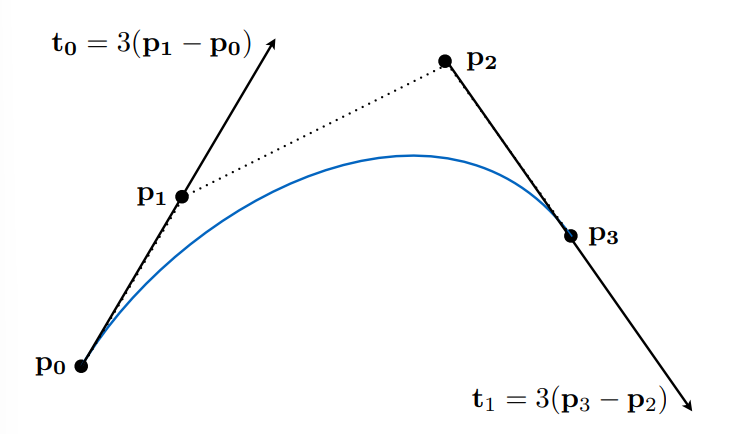
- 使用一系列的控制点定义某个曲线,控制点定义曲线满足的一些性质
- 可以定义出唯一的曲线,从 \(p_0\) 开始,\(p_3\) 结束
de Casteljau Algorithm 绘制贝塞尔曲线¶
- 给定任意多个控制点,生成贝塞尔曲线
对于两条线段,三个点的情况
- 使用线性插值的方式插入一个点
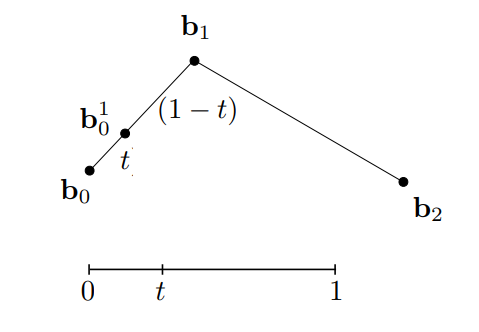
- 在另一条边等比例的插入另外一个点
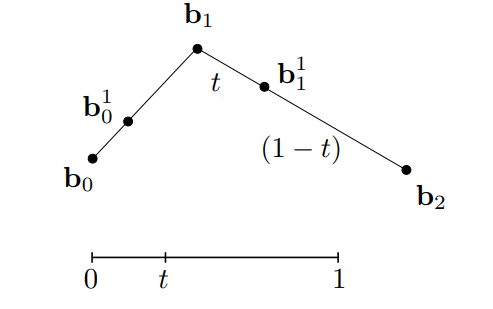
- 连接 \(b_0^1\) 和 \(b_1^1\) 得到 \(b_0^2\)
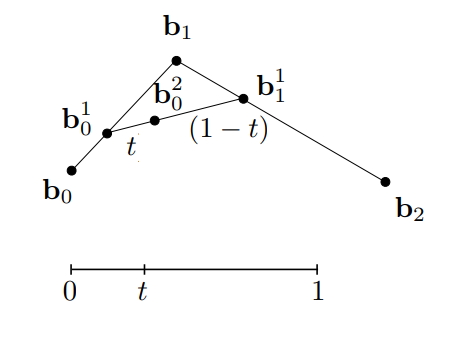
- 枚举 \([0,1]\) 中所有的参数 \(t\) ,连接所有得到的 \(b_0^2\) ,就获得了生成的曲线
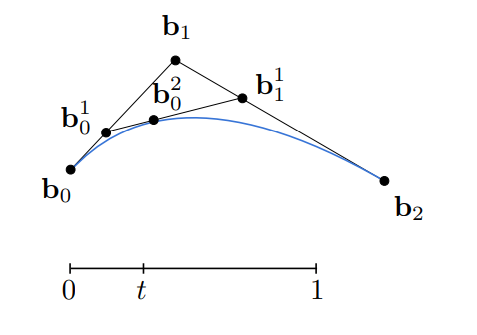
对于四条线段,三个点的情况,递归处理即可
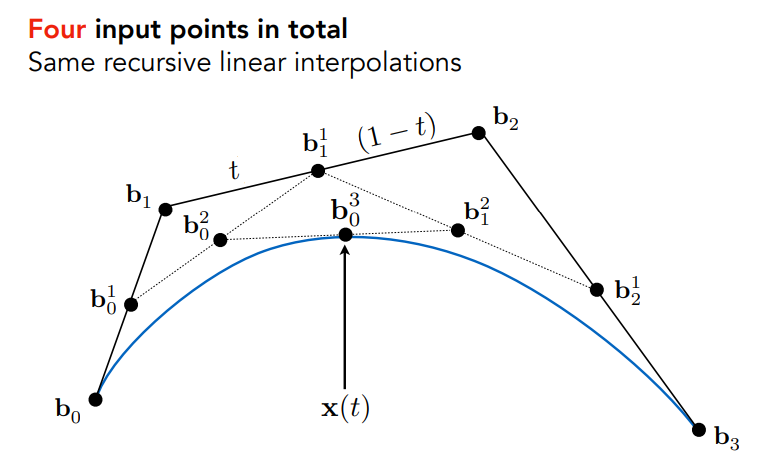
Algebraic Formula¶
e.g. 三个点的贝塞尔曲线的例子
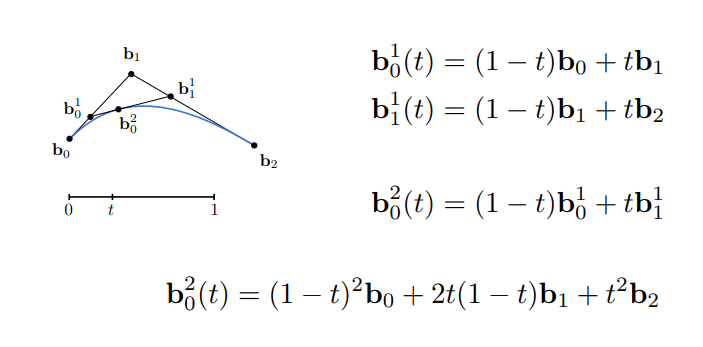
根据 \(b_0^1\) 和 \(b_1^1\) 得到 \(b_0^2\),将其展开容易得到上式,容易发现是系数是 \((1-t +t)^2\) 的形式,所以我们容易推理出贝塞尔曲线的一般代数表示
对于有 \(n+1\) 个点的贝塞尔曲线,在任意时间 \(t\),它都是给定的控制点的线性组合
\[
\mathbf{b}^n(t)=\mathbf{b}_0^n(t)=\sum_{j=0}^n \mathbf{b}_j B_j^n(t)
\]
其中,\(B_j^n(t)\) 是 Bernstein polynomial,描述为【就是描述 \((1-t +t)^n\) 的各项系数是多少】
\[
B_i^n(t)=\left(\begin{array}{c}
n \\
i
\end{array}\right) t^i(1-t)^{n-i}
\]
Features¶
- 对贝塞尔曲线的控制点做仿射变换(线性变换+平移)相当于对贝塞尔曲线做仿射变换
- 投影是不满足此性质
- 贝塞尔曲线的凸包性质:画出的贝塞尔曲线一定在几个控制点形成的凸包内
Piecewise Bézier Curves 逐段的贝塞尔曲线¶
当控制点较多时,贝塞尔曲线的形状不好控制。在实际的情况中,使用多段贝塞尔曲线进行首尾相接得到新曲线(一般使用四个控制点的三次贝塞尔曲线),这种方法就叫做逐段的贝塞尔曲线
Continuity 贝塞尔曲线的连续性¶
- \(C^0\) continuity:第一段的终止点和第二段的起点相接
- \(C^1\) continuity:导数连续,控制点的左右两个控制点方向相反,距离控制点的距离相等 \(\mathbf{a}_n=\mathbf{b}_0=\frac{1}{2}\left(\mathbf{a}_{n-1}+\mathbf{b}_1\right)\)
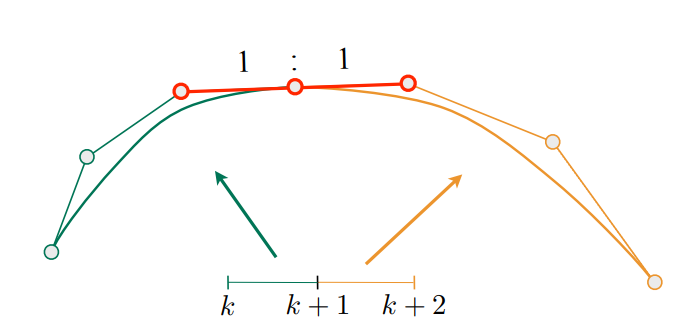
Spline 样条曲线¶
一个可控的曲线
B-splines B样条¶
- Short for basis splines 基函数(由不同函数组合成别的函数)样条
- 对贝塞尔曲线的扩展,当贝塞尔曲线的阶数高时,动一个点对周围的影响大,而 B 样条曲线具有局部性,更加容易控制
Surfaces¶
贝塞尔曲面¶
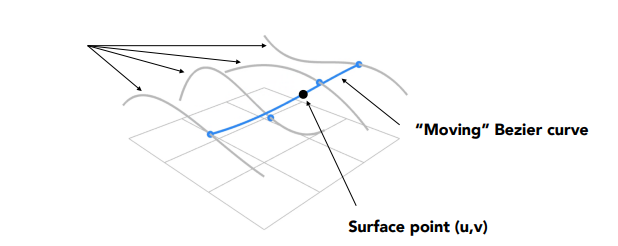
Evaluating Surface Position For Parameters \((u,v)\)
- Use de Casteljau to evaluate point \(u\) on each of the 4 Bezier curves in u. This gives 4 control points for the “moving” Bezier curve
- Use 1D de Casteljau to evaluate point v on the “moving” curve
Mesh Operations 曲面操作¶
- Mesh Subdivision (upsampling)
- Mesh Subdivision (upsampling)
- Decrease resolution
- try to preserve shape/appearance
- Mesh Regularization (same #triangles)
- Modify sample distribution to improve quality
Mesh Subdivision 细分¶
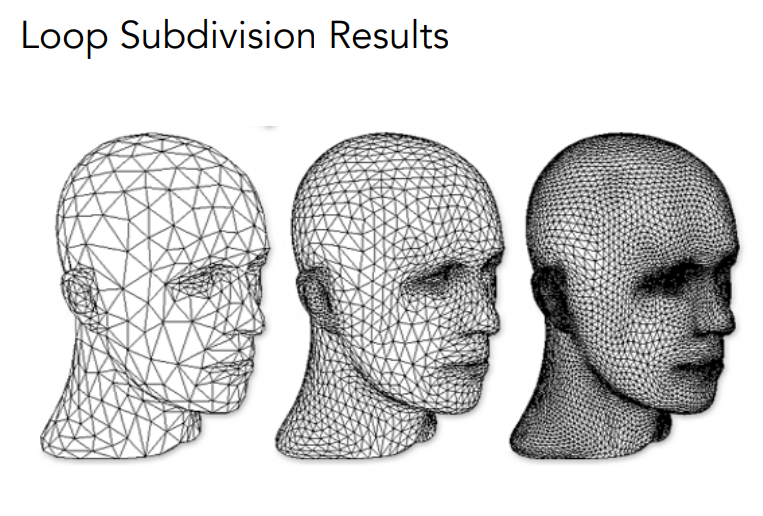
Loop Subdivision¶
- 只适用于三角形面
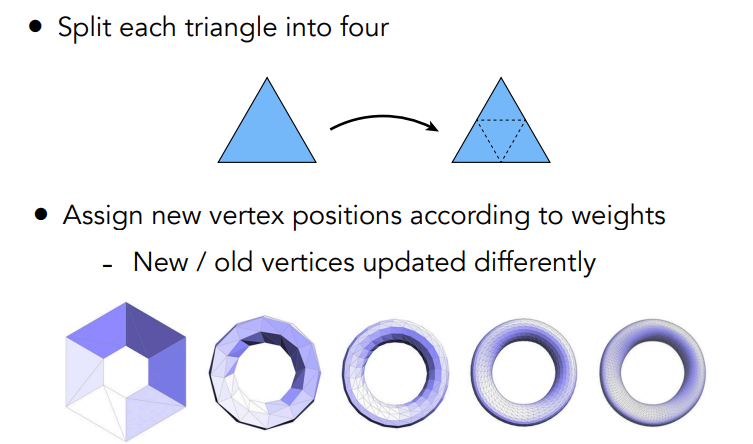
-
引入更多的三角形
- 连接原本三角形的三条边的中点,形成新的顶点
-
让三角形的位置发生一些变化,让原来的物体变得更加光滑
-
对于新的顶点
-
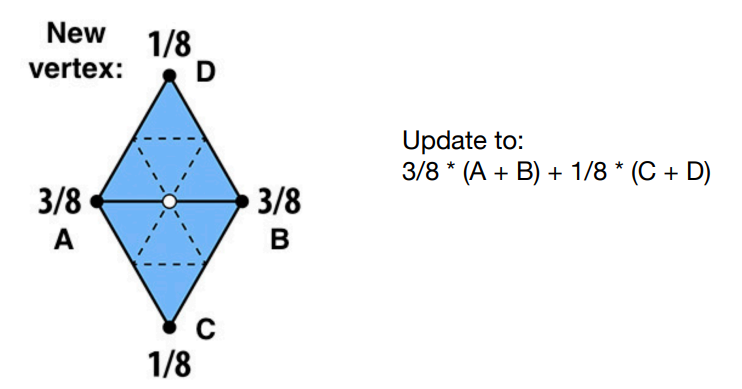
下图中的白色顶点为生成的新的顶点且被两个原三角形共享,认为 \(A,B\) 两点是距离白色点较近的两个点,\(C,D\) 两点是距离白色点较远的两个点,实质是一种加权平均,使得新出现的白点可以达到平滑的效果
-
Loop Subdivision 算法将白色顶点的坐标调整为
\[ \frac{3}{8}(A+B) + \frac{1}{8}(C+D) \] -
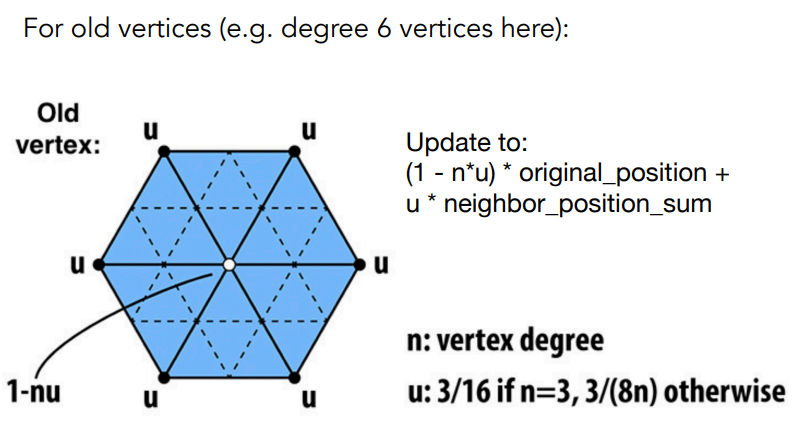
- 对于旧的顶点(虚线表示拆出的新三角形,老的顶点是中间的**白色**点)
- Loop Subdivision 算法使得调整后的新顶点,一部分相信老的顶点的平均值,一部分受新的顶点的影响
- 定义 $n$ 为白色顶点的度,下图中 $n=6$
- 定义 $u$ 为与 $n$ 有关系的一个数。当 $n=3$ 时,$u=\frac{3}{16}$,当 $n\ne 3$ 时,$u = \frac{3}{8n}$
- Loop Subdivision 算法将白色顶点的坐标调整为 (可以这么理解,如果一个顶点连了很多三角形,说明这个顶点可以由别人来决定,如果一个顶点连接的三角形数目很少,说明这个顶点自身比较重要,要更多的相信自己的信息)
$$
(1-un)\times \text{original-position} + u\times\text{neighbor-position-sum}
$$
Catmull-Clark Subdivision (General Mesh)¶
- 适用于一般的情况,网格不是三角形网格
- 非四边形面 (Non-quad face):不是四边形的面
- 奇异点/异顶点 (Extraordinary vertex):度不为 \(4\) 的顶点
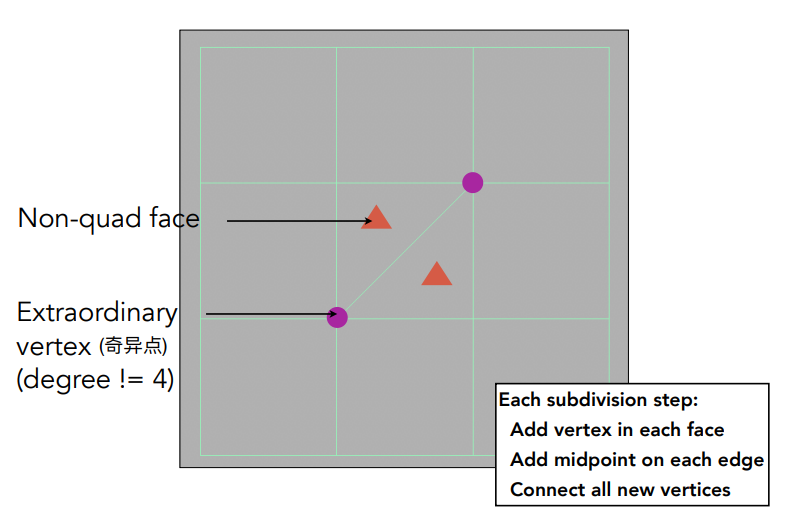
- 细分步骤
- 对所有的边和面取中点
- 将取出的中点连起来
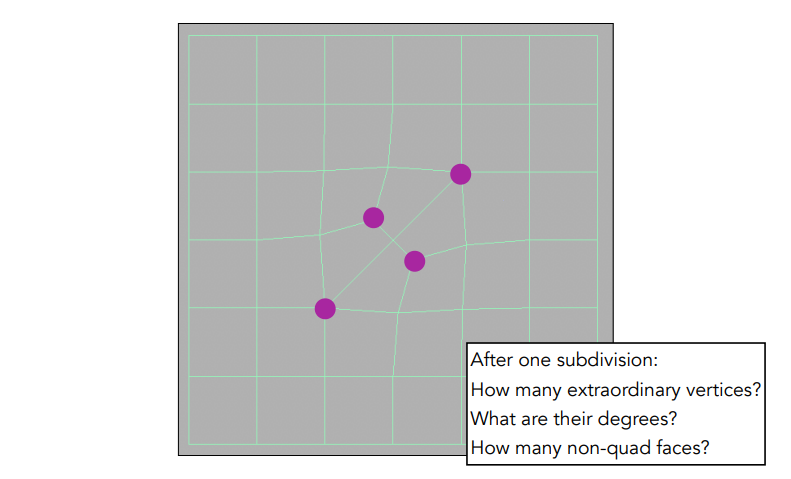
在一次细分之后,所有的非四边形面都消失了,每一个非四边形面都转化成了一个奇异点,之后奇异点的数目不会在增加了
- 调整步骤:将点区分成三类,分别更新他们的坐标
- 在一个面中心的新的点,设其为 \(f\)
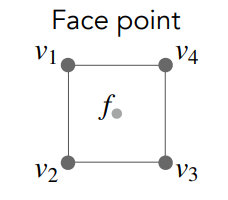
\[
f=\frac{v_1+v_2+v_3+v_4}{4}
\]
- 在边中心的新的点,设其为 \(e\)
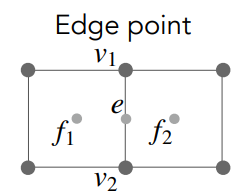
\[
e=\frac{v_1+v_2+f_1+f_2}{4}
\]
- 老的点,设其为 \(v\),定义 \(p\) 为老的点,\(m\) 为边的中点
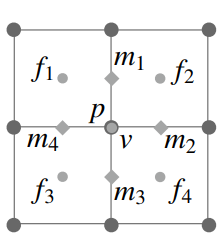
\[
v=\frac{f_1+f_2+f_3+f_4+2\left(m_1+m_2+m_3+m_4\right)+4 p}{16}
\]
Mesh Simplification¶
Edge Collapse 边坍缩¶
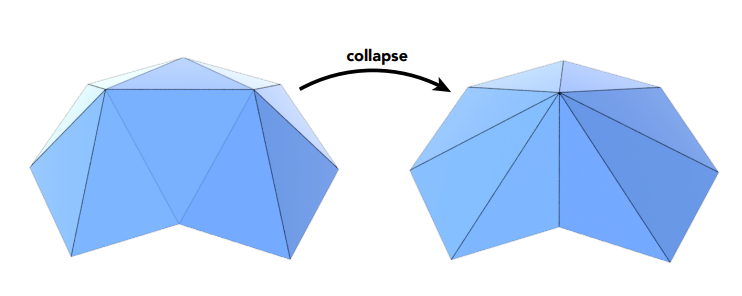
- 找到一条边,把连接这两条边的顶点变成一个顶点(捏起来)
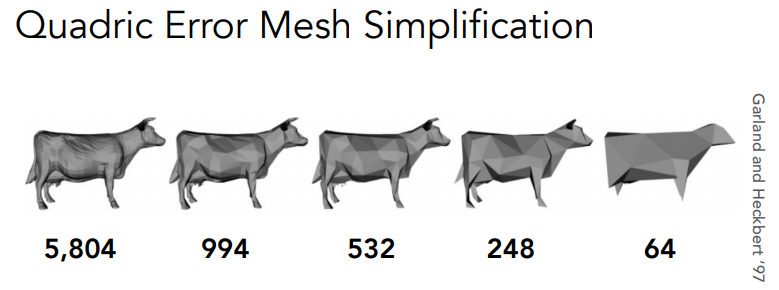
- 使用 Quadric Error Metrics(二次误差度量)来确定坍缩的边
- Quadric error: new vertex should minimize its sum of square distance (L2 distance) to previously related triangle planes
- 找到一个最优的位置,使得这个点到它原本的面的距离平方和最小
- 选择最优的边:优先队列
- 选取二次度量误差最小的边
- 合并这个边
- 更新所有受这个边影响的边
Shadow Mapping¶
- 如果有点在阴影里,就说明摄像机可以看到但光源看不到这个点
Algorithm¶
- Pass 1: Render from Light:从光源看向场景,记录光源能看到的深度图
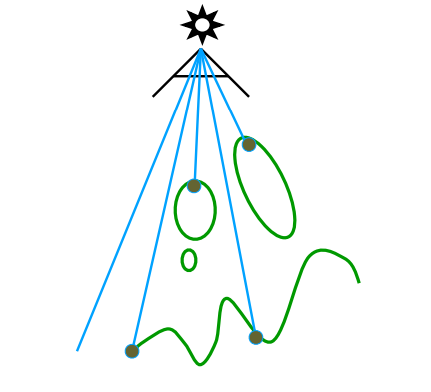
- Pass 2A: Render from Eye:从摄像机出发,看场景,记录摄像机能看到的深度图
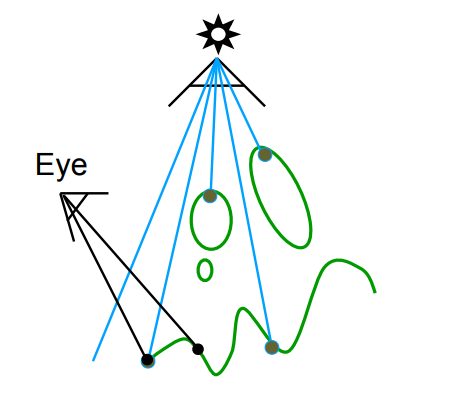
- Pass 2B: Project to light:把摄像机上看到的点投影回光源
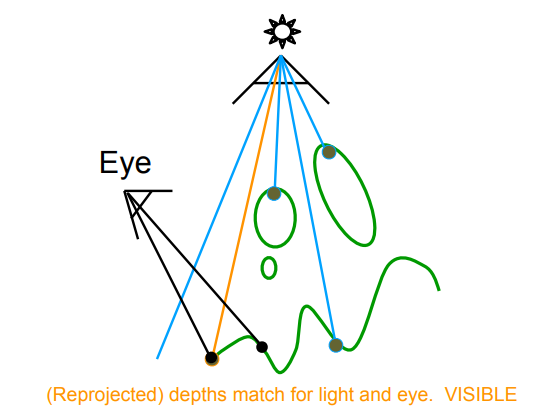
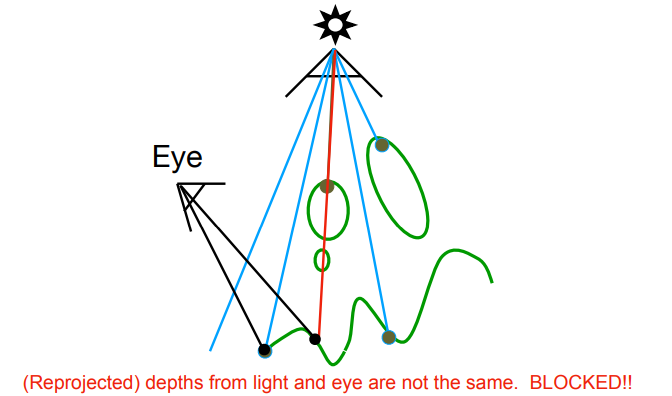
- 如果这个点反投影回光源的深度和光源一致,说明这个点对光源可见(橙色线)
- 如果不一致,说明这个点是阴影(红色线)
Cons¶
- 由于数值精度问题,判断两个距离是否相等时浮点数误差,导致阴影的边界不清晰
- 渲染两遍时的分辨率不同会导致误差,Shadow Map 的分辨率通常较低

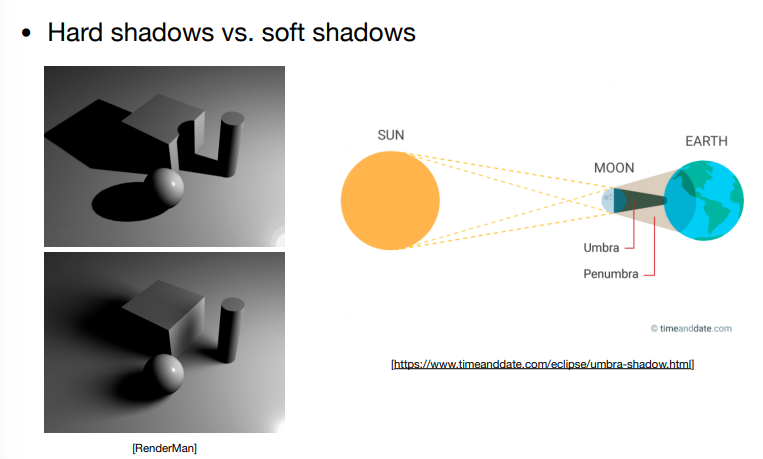
Hard Shadows vs. Soft Shadows¶
- 硬阴影:阴影的边界锐利
- 软阴影:边界不清晰,过渡明显
- 本影:一个位置完全看不到光源
- 半影:一个位置可以部分看到光源
- 对于点光源不可能出现软阴影,软阴影一定是光源具有一定大小造成的现象
Last update:
July 30, 2023
Created: June 16, 2023
Created: June 16, 2023