Lecture 07-09 Shading (Illumination, Shading, Graphics Pipeline and Texture Mapping)¶
Shading¶
定义¶
- The darkening or coloring of an illustration or diagram with parallel lines or a block of color.
- In this course: The process of applying a material to an object.

考虑任意一点的光照,定义以下几个概念,\(v,n,l\) 都表示方向,所以它们都是长度为 \(1\) 的单位向量
- Viewer direction, \(v\)
- Surface normal, \(n\)
- Light direction, \(l\) (for each of many lights)
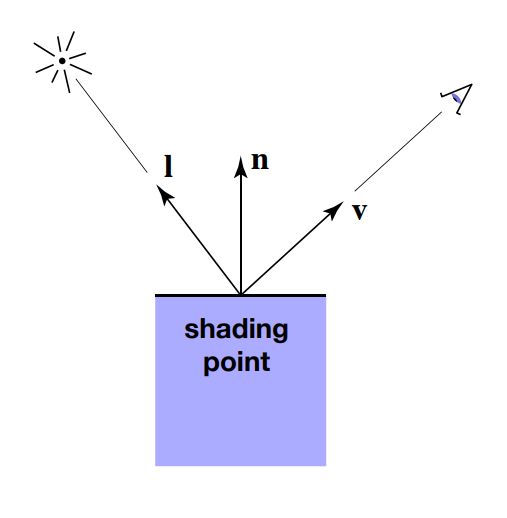
Shading is Local 着色具有局部性¶
- 这意味着我们只考虑它自己,也就是说考虑了明暗变换,不考虑阴影

Diffuse Reflection 漫反射¶
- 定义: 入射光会被均匀的反射到各个方向上的反射现象
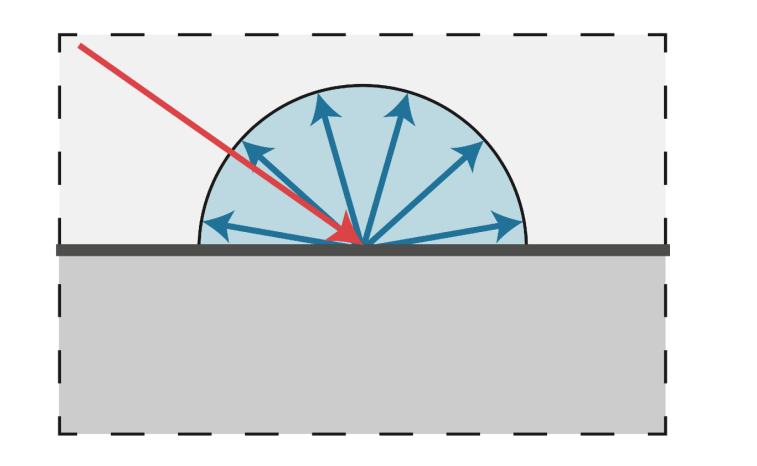
接收光的强度的计算¶
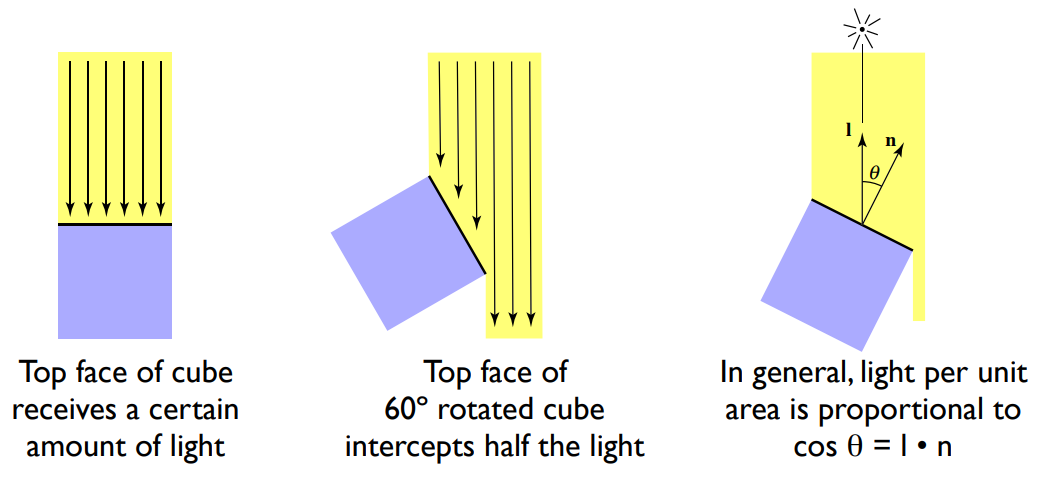
- Lambert’s cosine law: light per unit area is proportional to \(\cos\theta = l \times n\)
发射光强度的计算¶
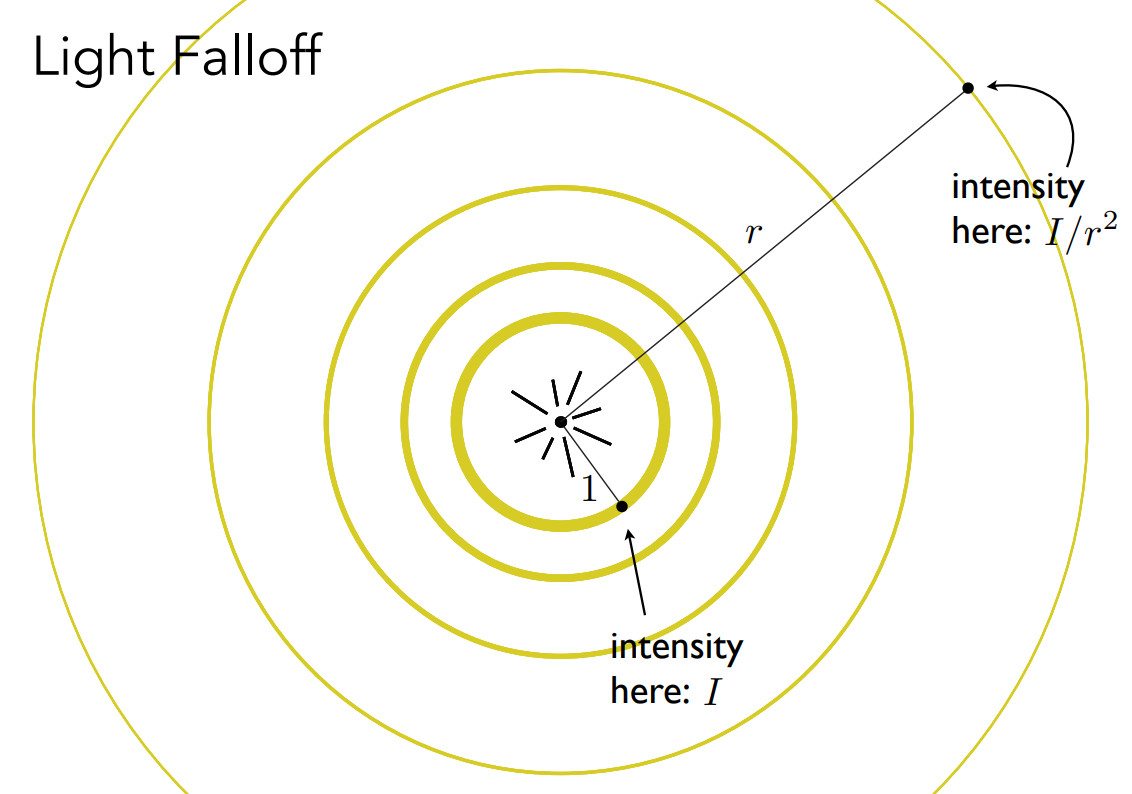
- 点光源辐射光的能量辐射在一个球壳上
Lambertian (Diffuse) Shading 漫反射¶
- 经验模型
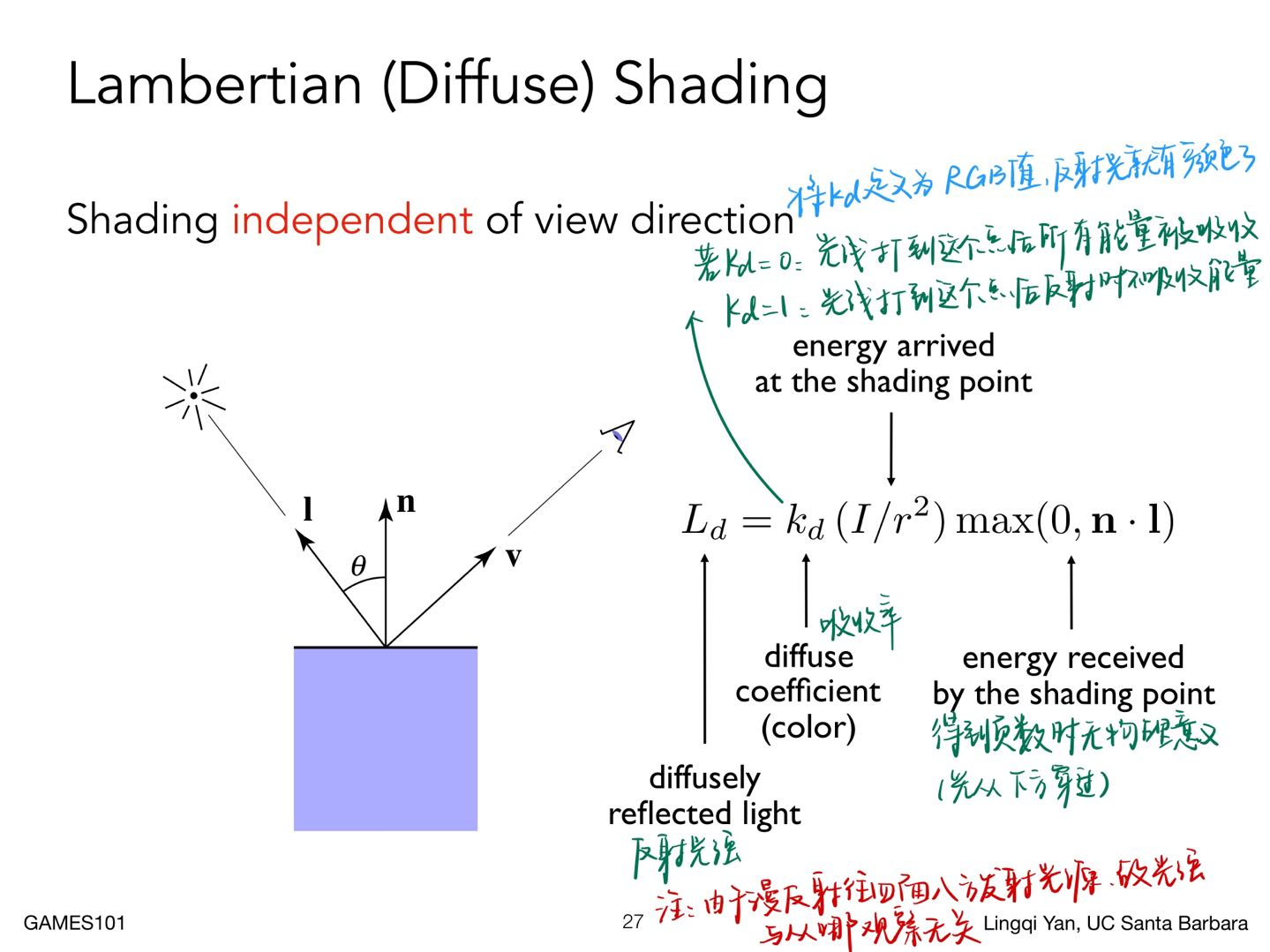
- 例子,光照球的弥散现象与 \(k_d\) 的关系

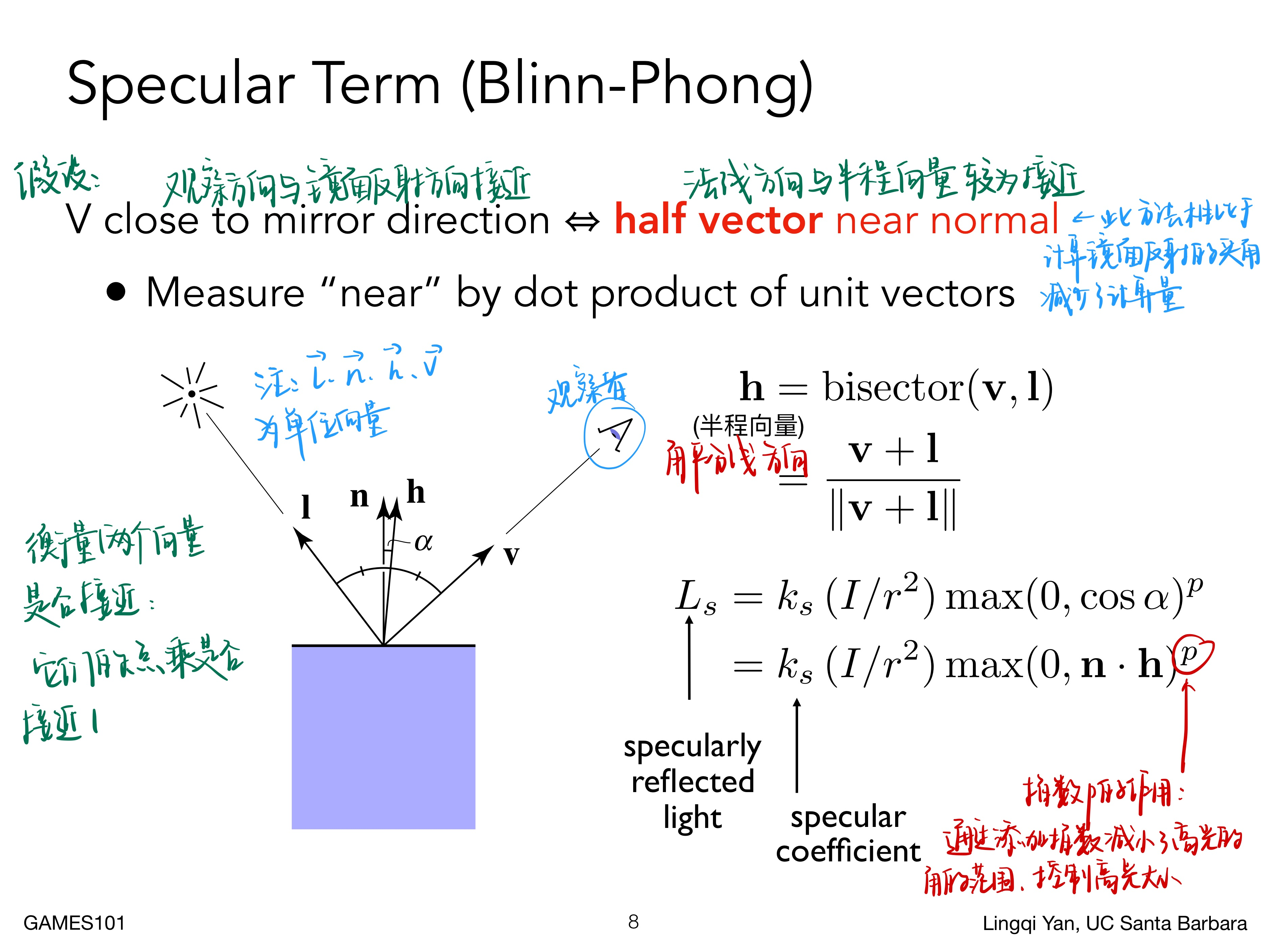
Specular Term 镜面反射¶
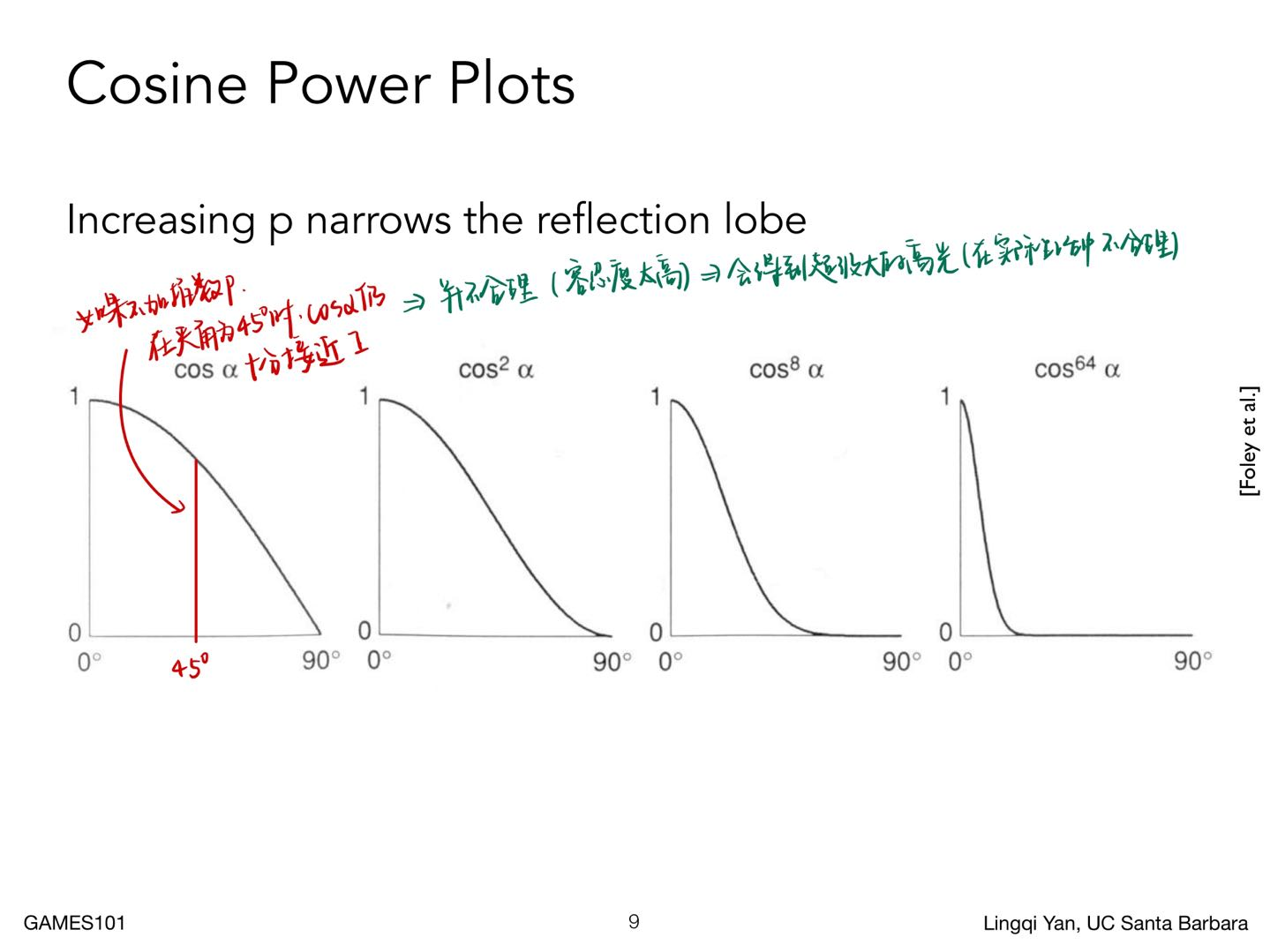
Cosine Power Plots¶
亮度 k 和高光指数 p 对高光的影响¶

Ambient Term 环境光照¶
- 因为环境光照太为复杂,所以认为环境光照和观察方向无关
- 但是这是大概的估计的计算

Blinn-Phong Reflection Model¶
- 布林冯反射模型由环境光照,漫反射和高光组成

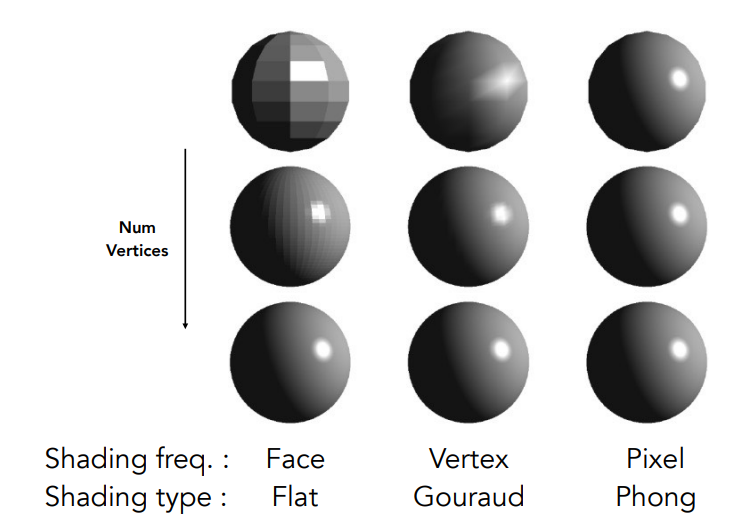
Shading Frequencies 着色频率¶

- Figure 1:一个平面做一次 Shading
- Figure 2:一个平面的四个顶点,算出四个对应的法线,对每个顶点做一次着色,对于三角形内部的点,对它们进行插值
- Figure 3:着色应用在每一个像素上
着色的类型¶
Flat shading 逐平面着色¶

Gouraud shading 逐顶点着色¶

Phong shading 逐像素着色¶

比较¶
- 当三角形面较多时,面密集时,使用 Flat Shading 效果不一定差
- 当三角形面非常多的时候(超过的了像素的数目),使用 Flat Shading 开销就比 Phong Shading 大了
- 所以不能说哪个着色模型一定效率高,或者哪个着色模型一定效果差
Defining Per-Pixel Normal Vectors 定义逐顶点的法线¶
- 如果知道了想表示什么,问题就简单了,例如要想表示一个球,那使用三角形构成的几何体的顶点的法线就从球心出发
- 使用临近的面的法线求平均值(根据面的面积加权求平均值)
- 根据顶点的法线求面上的法线 \(\to\) 重心坐标
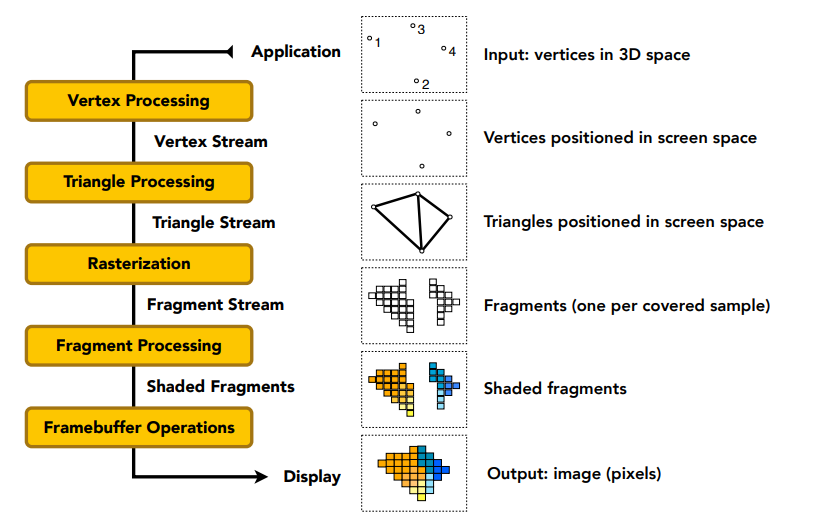
Graphics (Real-time Rendering) Pipeline 实时渲染管线¶
- 渲染管线:如何从场景到最后生成一张图的过程
- GPU: 图形渲染管线的硬件实现
- 着色器:是可编程的
- Heterogeneous, Multi-Core Processor
Shader Programs¶
- 只要管一个顶点或者一个像素怎么操作,描述对一个顶点(片段)的操作,不需要写 for 循环

Shading 2 (Texture Mapping)¶
Texture Mapping 纹理映射¶
- 希望得到一个三角形,三角形中填充了某一张图
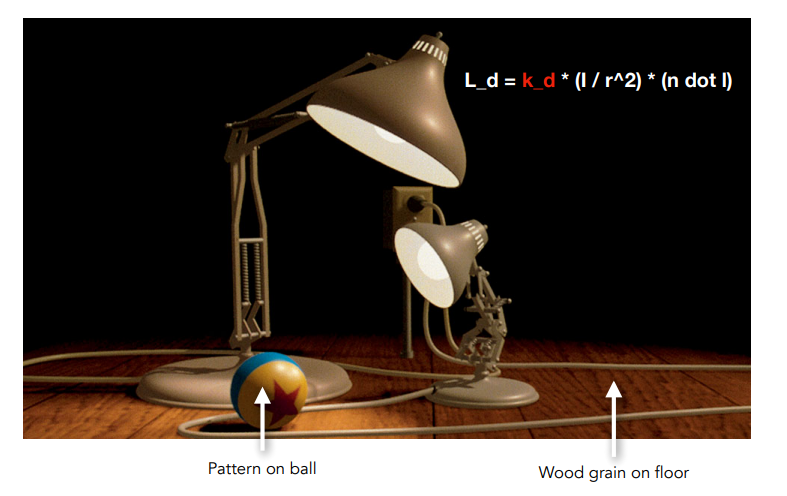
- 定义物体不同位置的不同属性 \(\to\) 定义任何一个点的属性 \(\to\) 改变 \(k_d\)
Surfaces are 2D¶
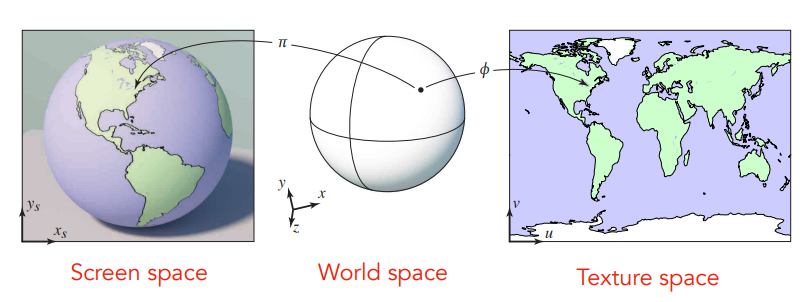
- 可以认为,三维物体的表面是二维的
- 任何一个三角形的都能在纹理空间中找到映射(认为已知)
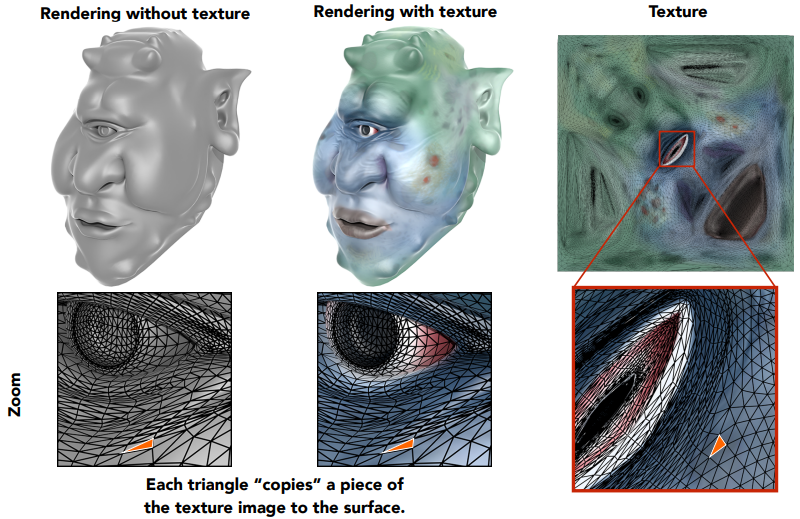
- 通常用 \((u,v)\) 表示纹理坐标系,规定 \(u,v \in (0, 1)\)
- 在下图中,绿色表示在 \(v\) 方向上数值大,红色表示在 \(u\) 方向上数值大
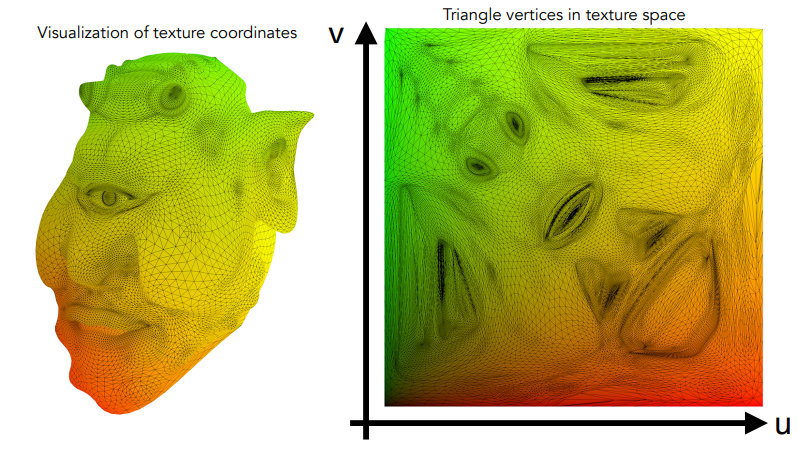
- 纹理可以被不停的重复
- 如果纹理设计的好,可以无缝衔接(tileable texture 无缝纹理)


Interpolation Across Triangles: Barycentric Coordinates 在三角形内插值:重心坐标¶
- 重心坐标:目的是做三角形内的插值
- 插值的意义:知道顶点的属性之后,获得在三角形内的平滑过渡(从一个顶点过渡到另外一个顶点)
- 插值的对象(都是三角形顶点的属性):材质、颜色、法线
Barycentric Coordinates 重心坐标¶
对于三角形所在任意平面上的一个点 \((x,y)\) 都可以用以下线性组合表示
- 如果点在三角形内,需要满足 \(\alpha,\beta,\gamma>0\)
- 根据重心坐标的定义,三角形顶点本身的重心坐标很容易得到,如下图
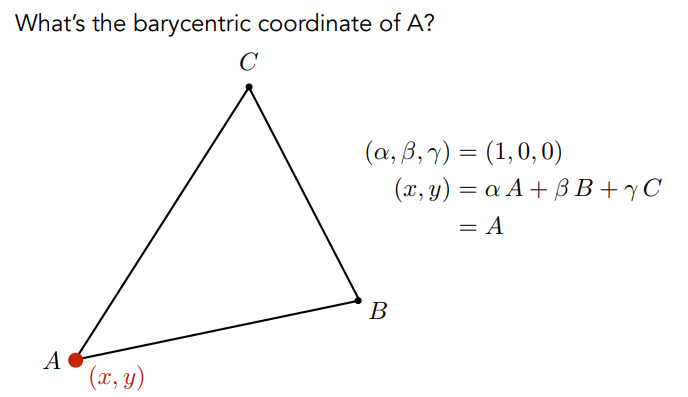
- 【重心坐标的另一个定义】对于任意点的重心坐标,可以通过面积比求出
- 对于三角形的重心,很容易得到三角形的重心的重心坐标为 \((x, y)=\frac{1}{3} A+\frac{1}{3} B+\frac{1}{3} C\)
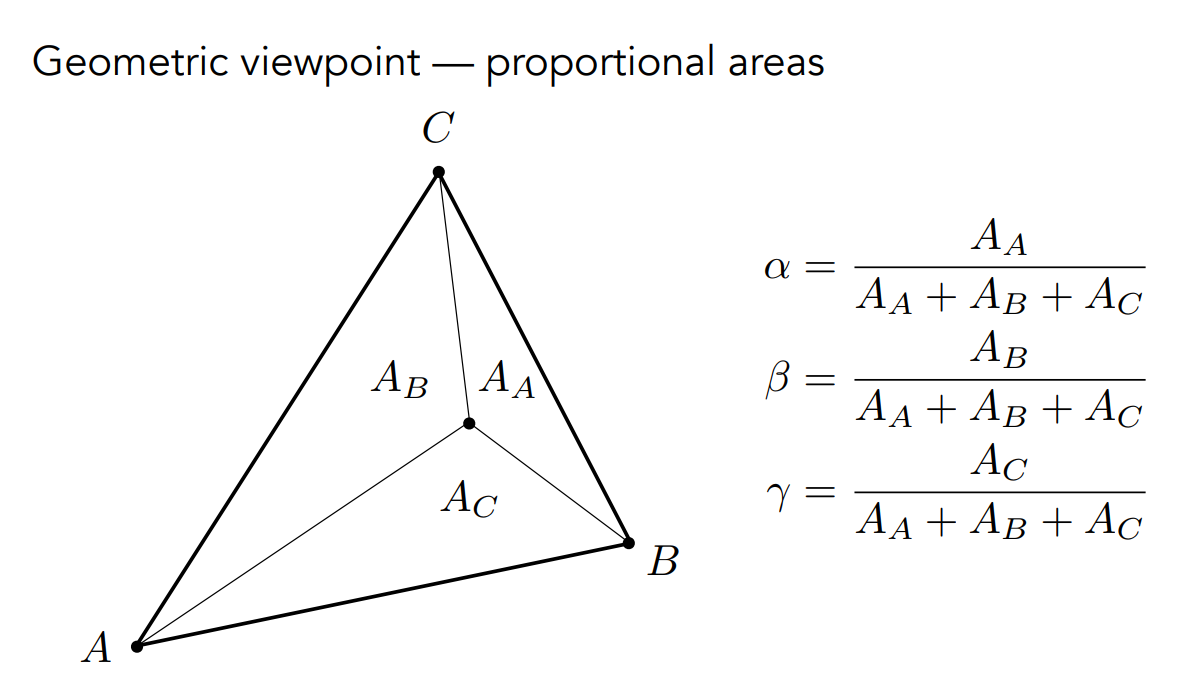
对于重心坐标,有以下的一般表达式
- 【注意】重心坐标并不在投影下保持不变,如果要插值三维空间的图形,需要在投影前在三维的空间中进行插值
Using Barycentric Coordinates¶
for each rasterized screen sample (x,y):
(u,v) = evaluate texture coordinate at (x,y)
texcolor = texture.sample(u,v); // 在纹理图上查询
set sample’s color to texcolor; // 认为纹理定义的是漫反射系数
Texture Magnification(Easy Case: too small) 纹理放大¶
在纹理太小的时候(纹理分辨率低),但是屏幕是高分辨率的,采样时会采样到非整数点 \(\to\) 最简单的方法:四舍五入(Nearest)
A pixel(生成的屏幕上的像素) on a texture — a texel (纹理元素、纹素)

Bilinear Interpolation 双线性插值¶
- 定义一维的插值函数 \(\operatorname{lerp}\left(x, v_0, v_1\right)\)
- \(\operatorname{lerp}\left(x, v_0, v_1\right)=v_0+x\left(v_1-v_0\right)\)
- 在水平方向插值得到两对点 helper lerps
- \(u_0=\operatorname{lerp}\left(s, u_{00}, u_{10}\right)\)
- \(u_1=\operatorname{lerp}\left(s, u_{01}, u_{11}\right)\)
- 使用插值得到的两个点做竖直插值,得到最终结果
- \(f(x, y)=\operatorname{lerp}\left(t, u_0, u_1\right)\)
这样,插值得到的点综合考虑了它临近的四个点
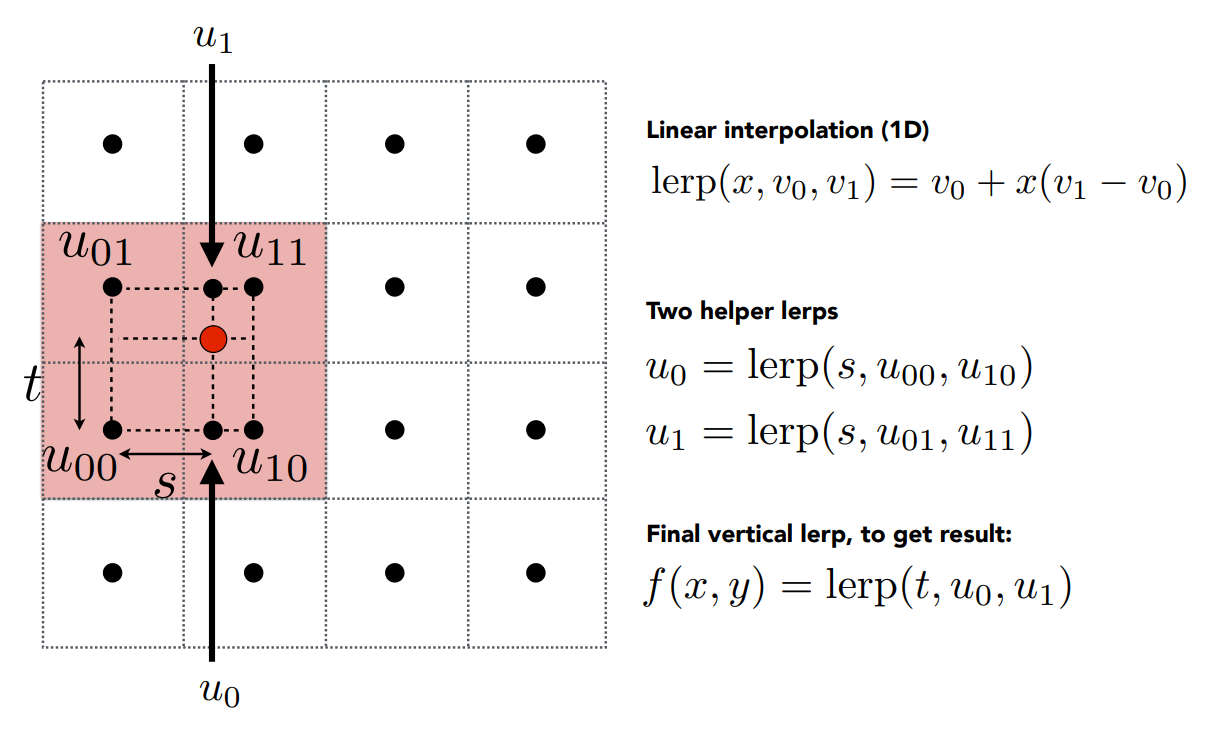
Bicubic Interpolation 双三次插值¶
取临近的 \(16\) 个点,运算量大
Texture Magnification(Hard Case: too large)¶
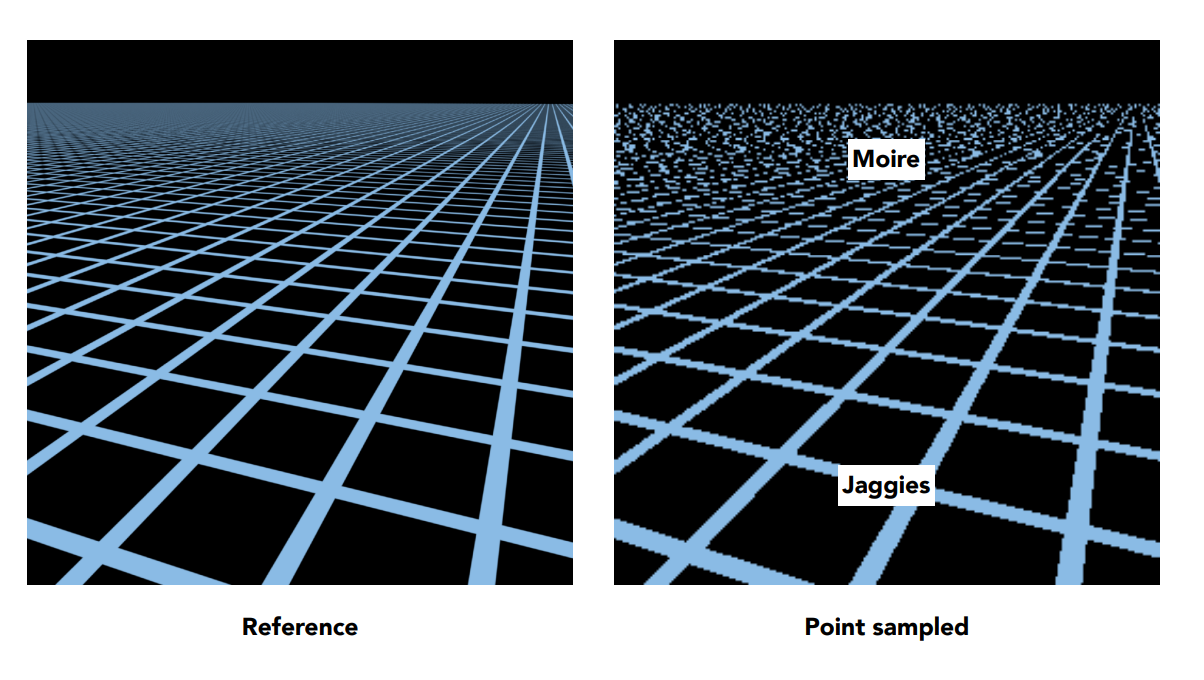
产生这种现象的原因:一个像素覆盖的纹理范围太大了(如下图)
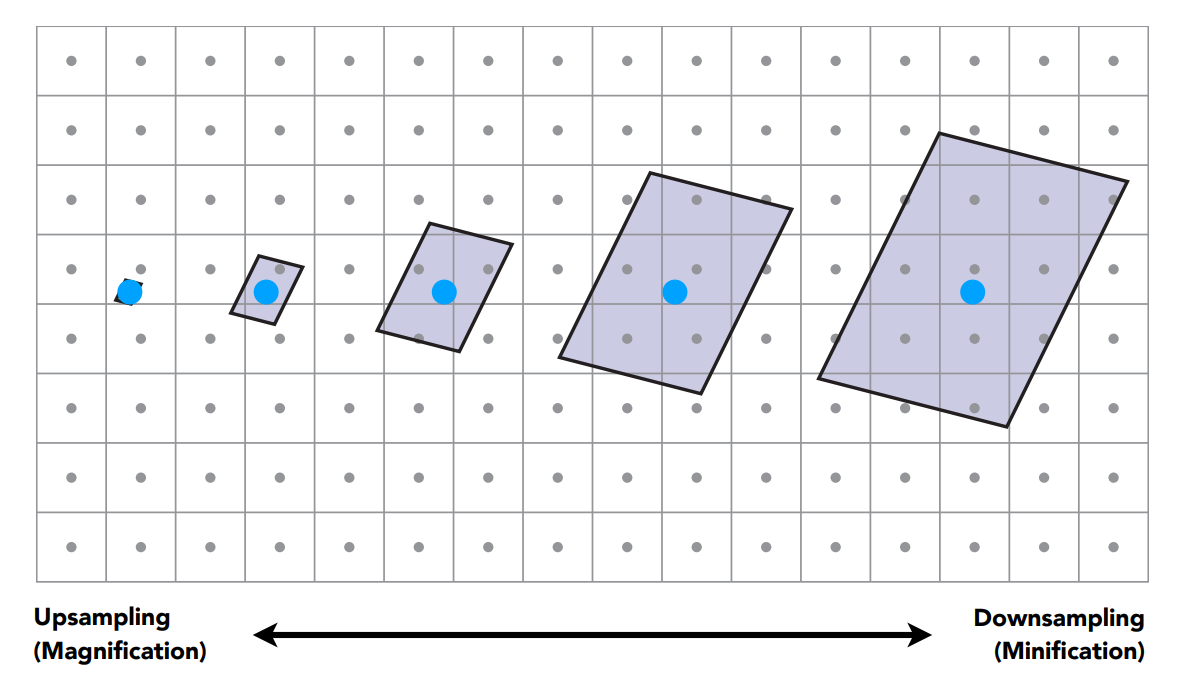
因此,我们不能简单地使用像素中心进行采样
可以使用超采样,但是开销太大 \(\to\) 使用范围查询方法
Mipmap¶
- Allowing (fast, approx., square) range queries
- Mipmap 提供的范围查询是近似的
- Mipmap 只能做正方形的范围查询
- 只引入了 \(\frac{1}{3}\) 的额外存储空间

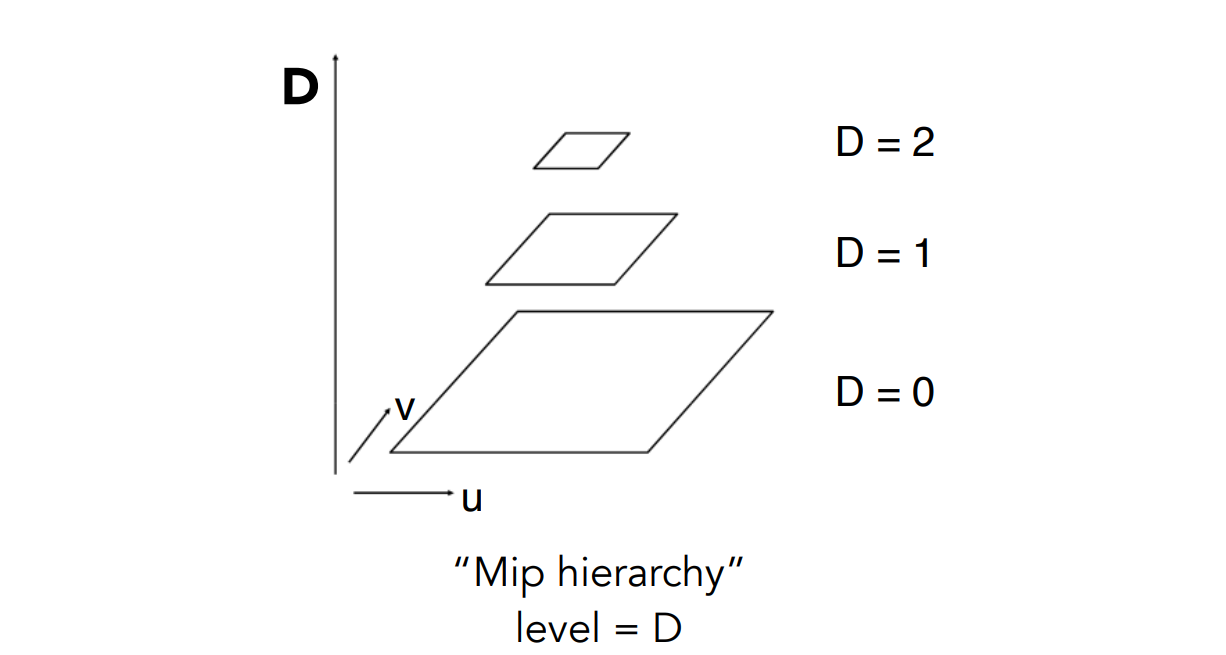
Computing Mipmap Level D¶
计算屏幕上两个像素之间的距离应当等价于纹理空间中的多少距离,根据这个距离求应该应用哪一层的 Mipmap
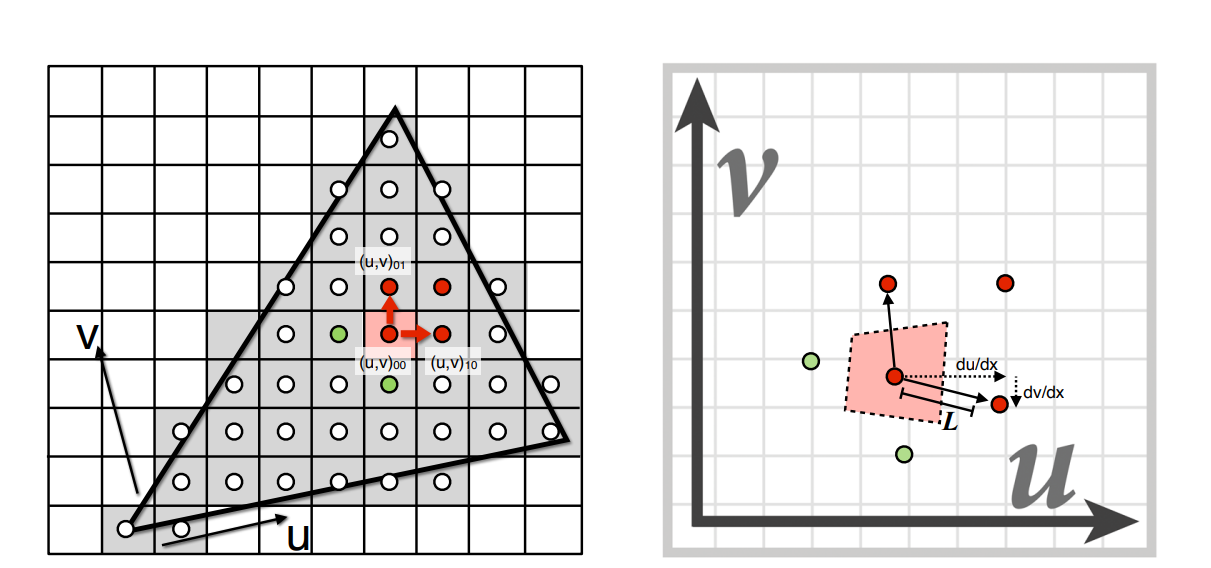 \(\(
D=\log _2 L \quad L=\max \left(\sqrt{\left(\frac{d u}{d x}\right)^2+\left(\frac{d v}{d x}\right)^2}, \sqrt{\left(\frac{d u}{d y}\right)^2+\left(\frac{d v}{d y}\right)^2}\right)
\)\)
\(\(
D=\log _2 L \quad L=\max \left(\sqrt{\left(\frac{d u}{d x}\right)^2+\left(\frac{d v}{d x}\right)^2}, \sqrt{\left(\frac{d u}{d y}\right)^2+\left(\frac{d v}{d y}\right)^2}\right)
\)\)
Visualization of Mipmap Level¶

在对一个区域的 Mipmap 做可视化之后,发现得到的 Mipmap 并不连续,于是需要引入插值来解决这一问题
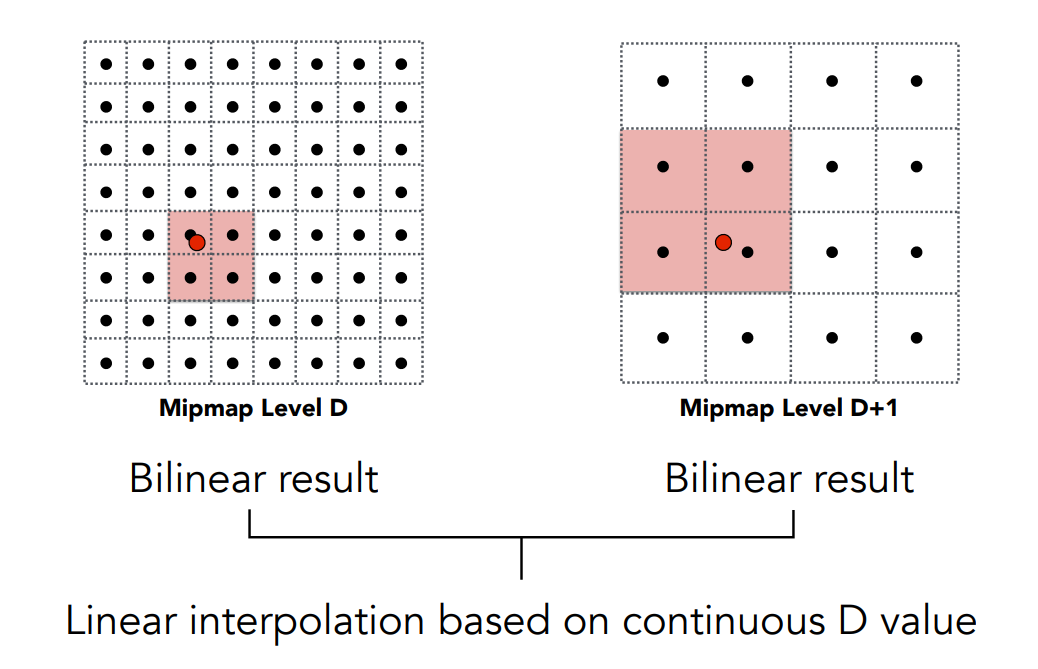
Trilinear Interpolation 三线性插值¶
求第 \(D\) 层和第 \(D+1\) 层的双线性插值(Mipmap 查询),再在两层之间做线性插值,以得到平滑的效果

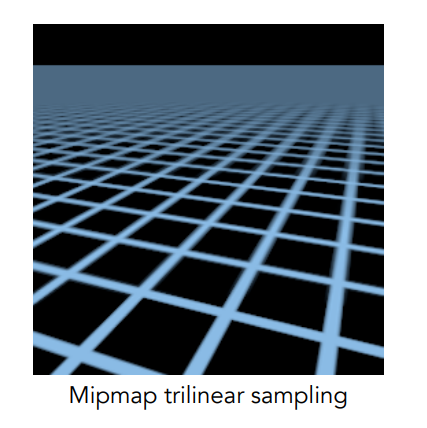
Mipmap Limitations¶
Mipmap 在远处出现 Overblur 现象(过度模糊)
原因是 Mipmap 只能对正方形范围进行查询,但在实际中,映射在纹理空间的区域不一定为正方形
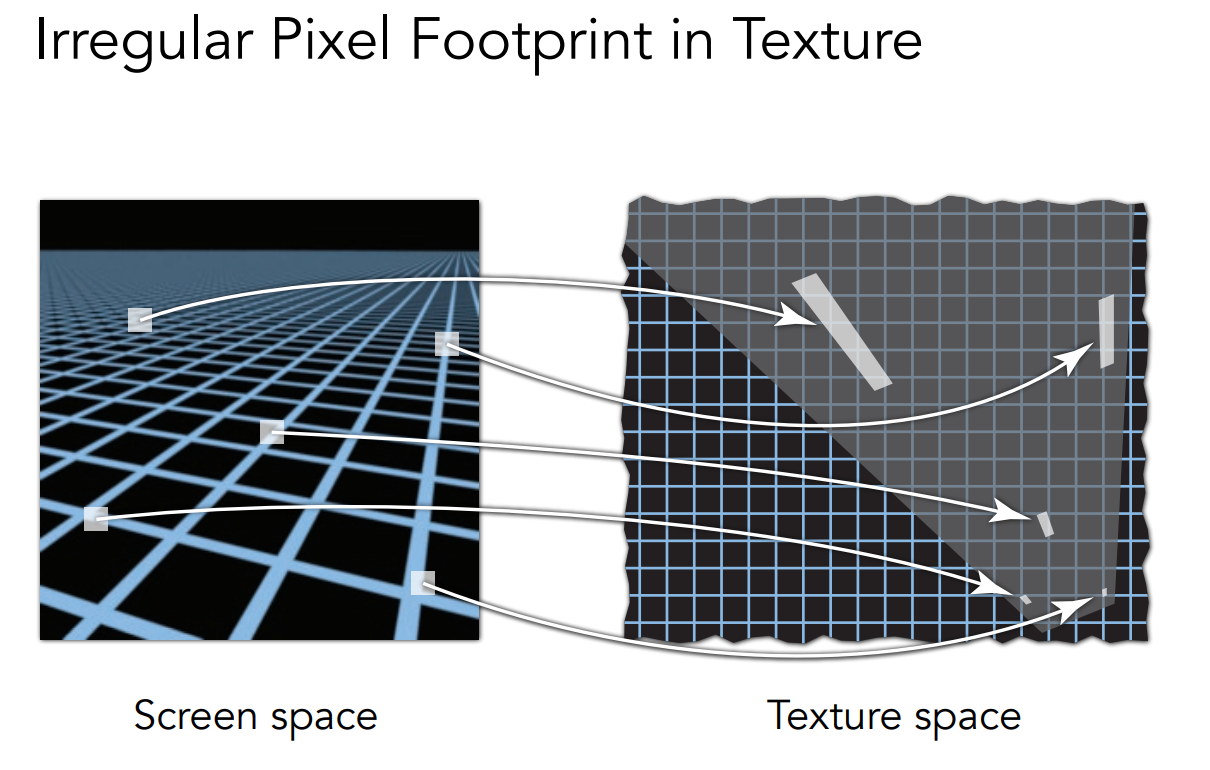
Anisotropic Filtering 各向异性过滤¶
- 在引入各向异性过滤之后,可以对矩形区域进行范围查询,可以得到更准确的结果
- 但是对于斜着的矩形区域,还是不能得到很好的插值
- 开销是原本的三倍
- 各向异性:在不同方向上表现不同

各向异性过滤得到的效果图
\(nx\) 各向异性过滤表示过滤 \(n\) 次,当 \(n\to \infin\) 时,空间开销会收敛为原本的三倍,对于显存有所要求,但在性能上影响很小
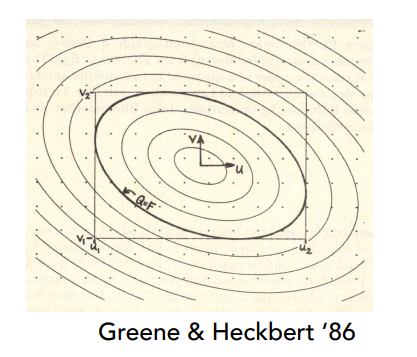
EWA filtering¶
- 对于任意不规则形状,可以拆成很多不同的圆形,来覆盖这个不规则的形状,进行多次查询来近似
Application of Texture Mapping¶
描述环境光照¶
- 使用 Texture Mapping 表述环境光照:描述来自不同方向的光照信息
- 犹他茶壶

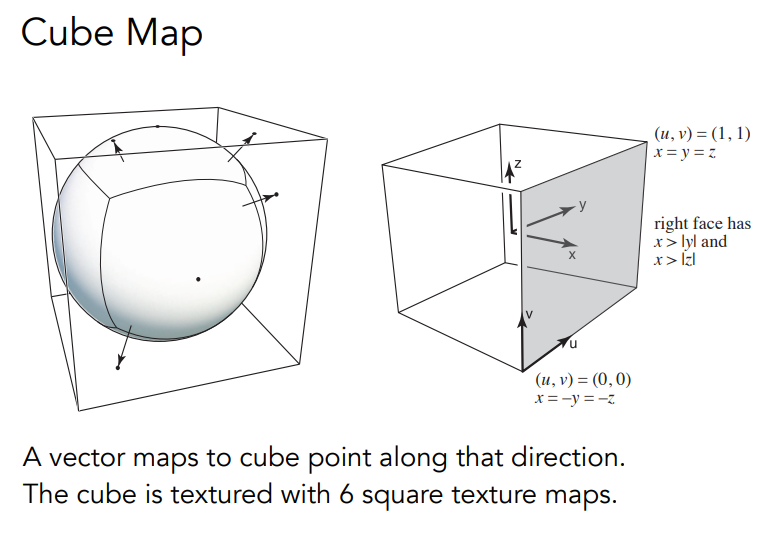
- 使用球来记录环境光照
- 存在的问题:将球的材质展开之后会产生扭曲现象
- 解决方法:使用球的外层包围盒的立方体记录环境光照,但是需要 dir \(\to\) face computation

法线贴图¶
- 纹理可以定义不同位置的不同属性:法线贴图
- 表面的凹凸特性(相对高度)
- 通过法线贴图,可以定义复杂的纹理但是不改变任何的几何信息(不改变三角形个数)

-
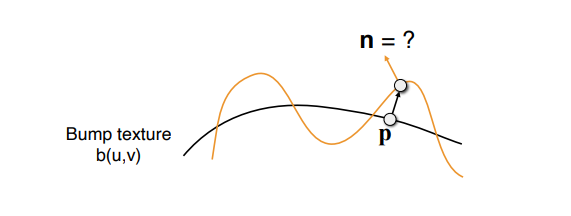
Bump Mapping 凹凸贴图
- 对于任何一个像素的法线进行扰动
- 通过临近位置的高度差来重新计算法线,通过相对高度的变化改变法线
-
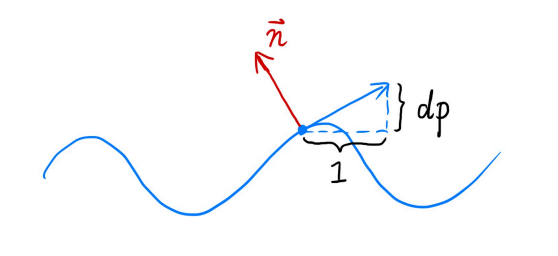
计算凹凸贴图生成的新法线(二维情况)
- 构建局部坐标系,认为原本在 \(p\) 点的法线是 \(n(p)=(0,1)\)
- 计算曲线上的切线,定义常数 \(c\) 为凹凸贴图的影响程度,那么根据差分方法有 \(dp = c\times [h(p+1)-h(p)]\)
- 将切线变为法线,法线垂直于切线,上一步求出的切线是 \(n(p) = (1, dp)\),将这个切线逆时针旋转 \(90\) 度,得到的法线为 \(n(p') = (-dp, 1)\),再将其规范化即可
-
计算凹凸贴图生成的新法线(三维情况)
- 构建局部坐标系,认为原本在 \(p\) 点的法线是 \(n(p)=(0,0,1)\)
- 求 \(p\) 点在两个方向 \(u,v\) 的切线
- \(dp/du = c_1 \times [h(u+1) - h(u)]\)
- \(dp/dv = c_2 \times [h(v+1) - h(v)]\)
-
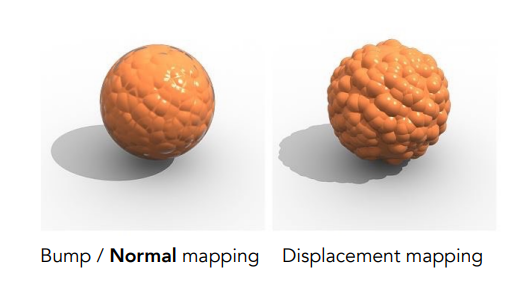
Displacement mapping 位移贴图
- 使用和凹凸贴图同样的材质
- 三角形的顶点有真的位置移动
- 位移贴图需要足够细致的三角形,三角形的频率要比纹理频率高
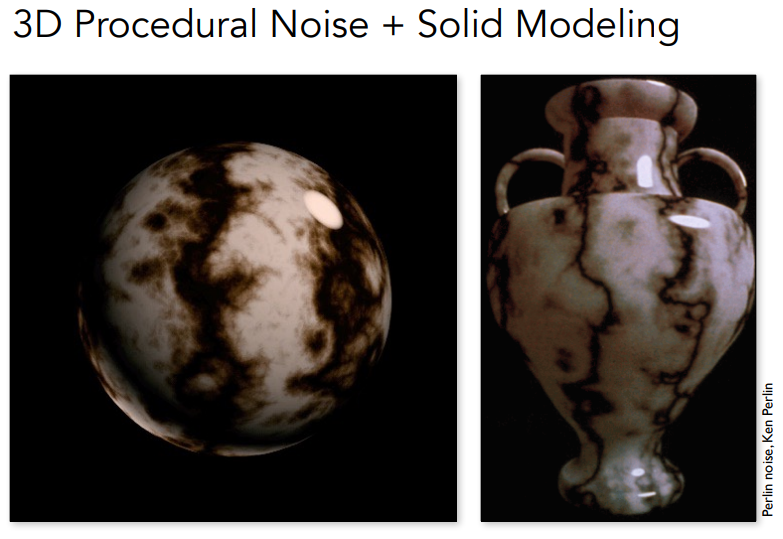
3D Procedural Noise¶
- 通过定义噪声函数计算出三维空间中的每一个点的噪声值,不仅提供了物体表面的纹理信息,还给出了物体内部的纹理信息
- 柏林噪声(Perlin noise)是最常见的噪声函数之一
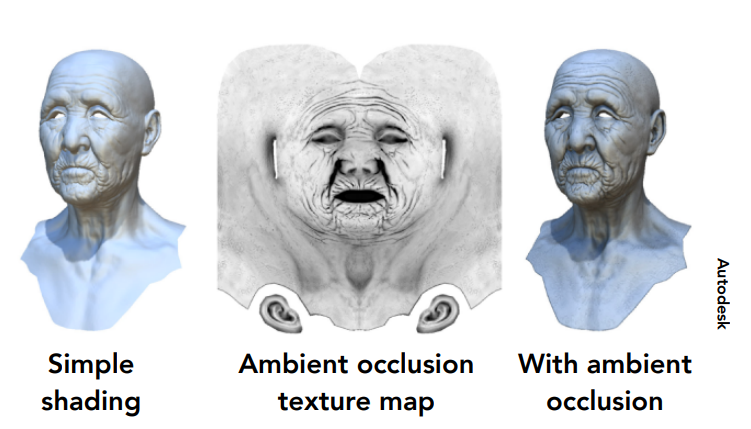
提供预计算的着色信息¶
- Ambient occlusion:环境光遮蔽
- 将环境光遮蔽信息存储到纹理中
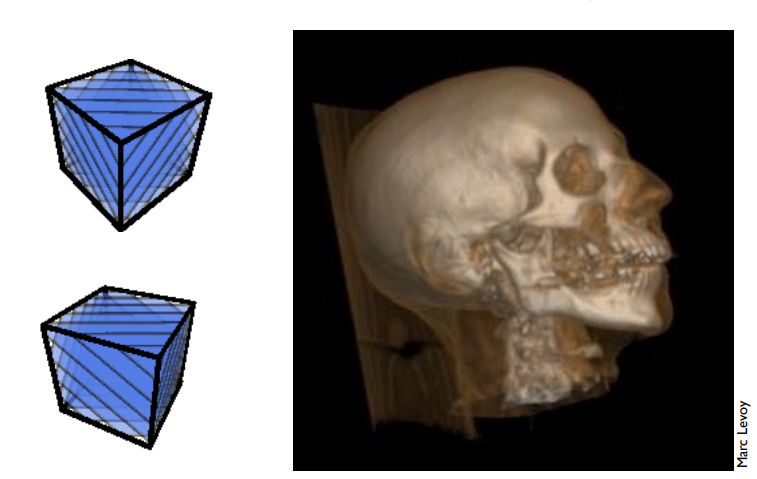
三维纹理和体积渲染¶
- 应用于 CT MRI
Created: June 16, 2023