Lecture 06 Rasterization 2 (Antialiasing and Z-Buffering)¶
Sampling theory¶
Sampling Artifacts in Computer Graphics¶
- Aliasing 锯齿

- Moiré Patterns in Imaging 摩尔纹

- Wagon Wheel Illusion (False Motion) 车轮效应
对于旋转方向的错误感知

-
Artifacts due to sampling - "Aliasing"
-
Jaggies – sampling in space
-
Moire – under sampling images
-
Wagon wheel effect – sampling in time
-
原因:信号变化的速度太快了但采样太慢了
Blurring (Pre-Filtering) Before Sampling 在采样前模糊¶
- 原始的采样
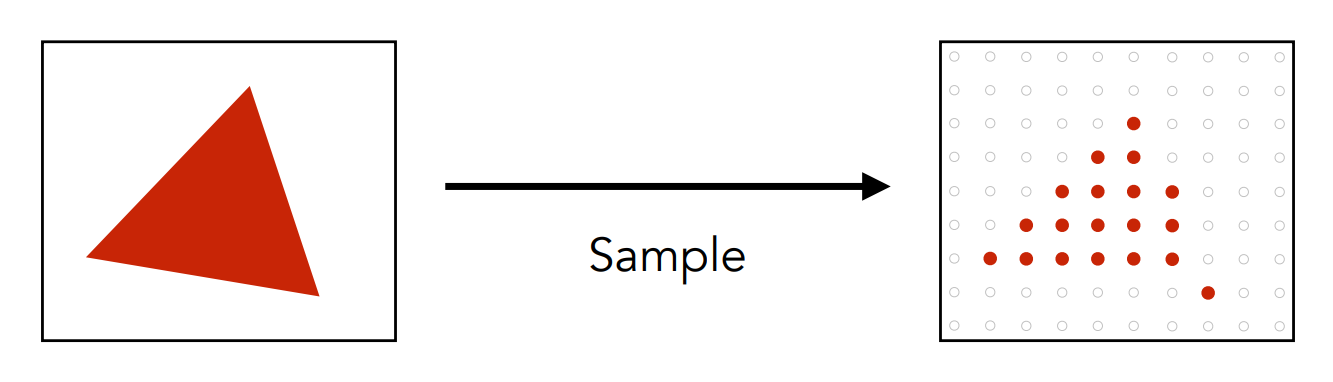
- 经过模糊(滤波)后的采样
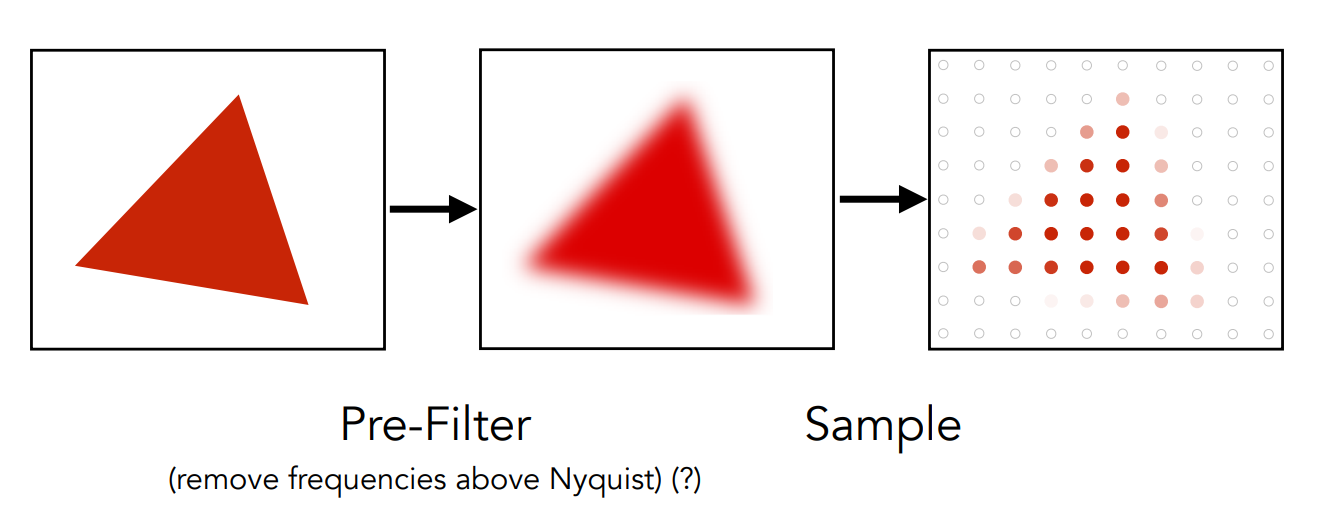
- 在实际应用中的效果

- 注意:不能先采样再做模糊,会导致锯齿被模糊

Frequency Domain 频域¶
Frequencies¶
- 定义 \(\cos 2\pi fx\) 中的 \(f\) 为频率
- \(f=\frac{1}{T}\)
Fourier Transform 傅里叶变换¶
- 任何周期函数都可以被展开为 \(\sin x\) 和 \(\cos x\) 的和的形式
- 把图像从时域(图像空间)变为频域(频率空间)
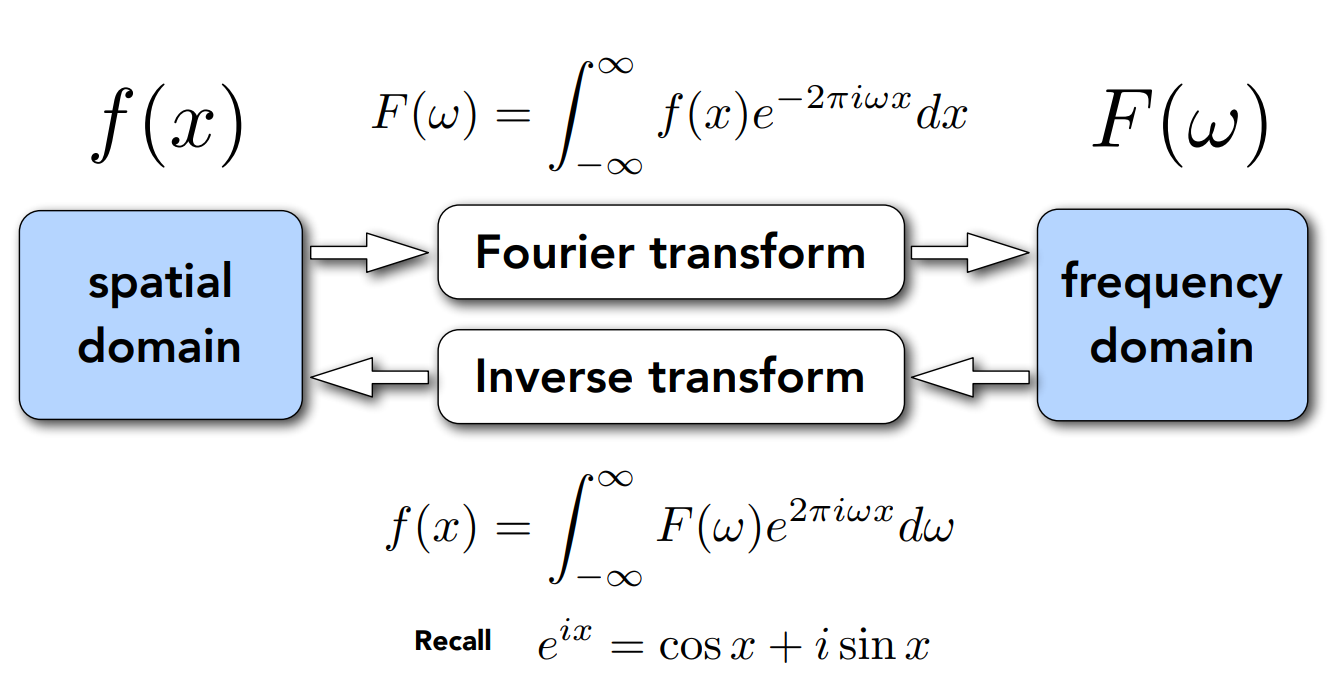
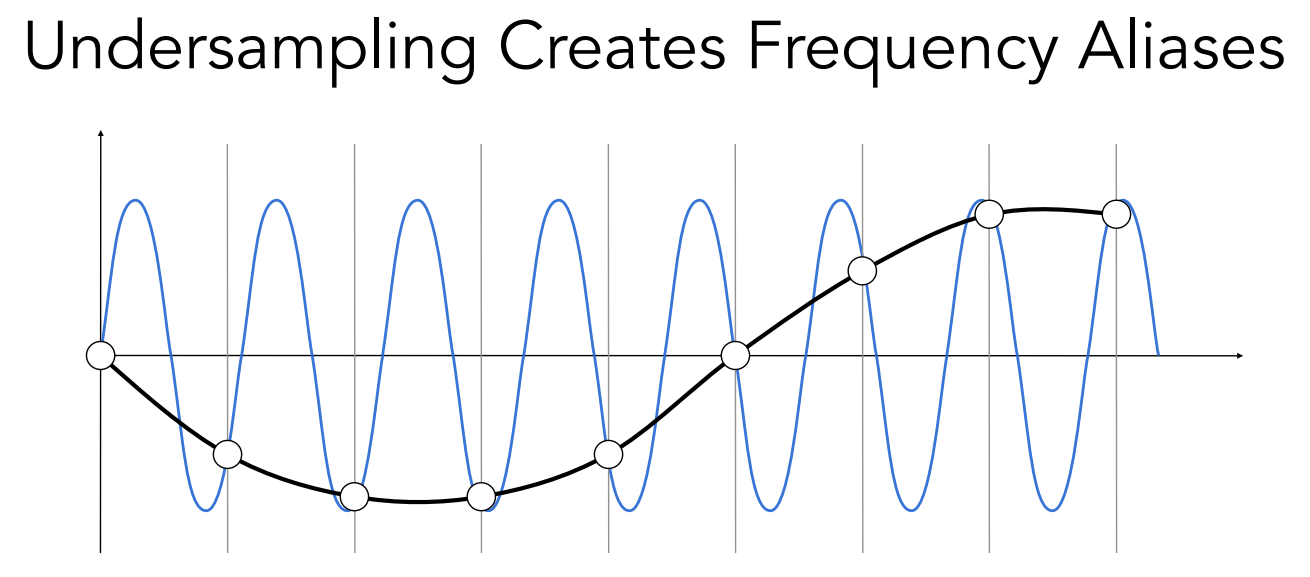
在这样的条件下,可以发现,频率越高的函数需要更高的采样频率
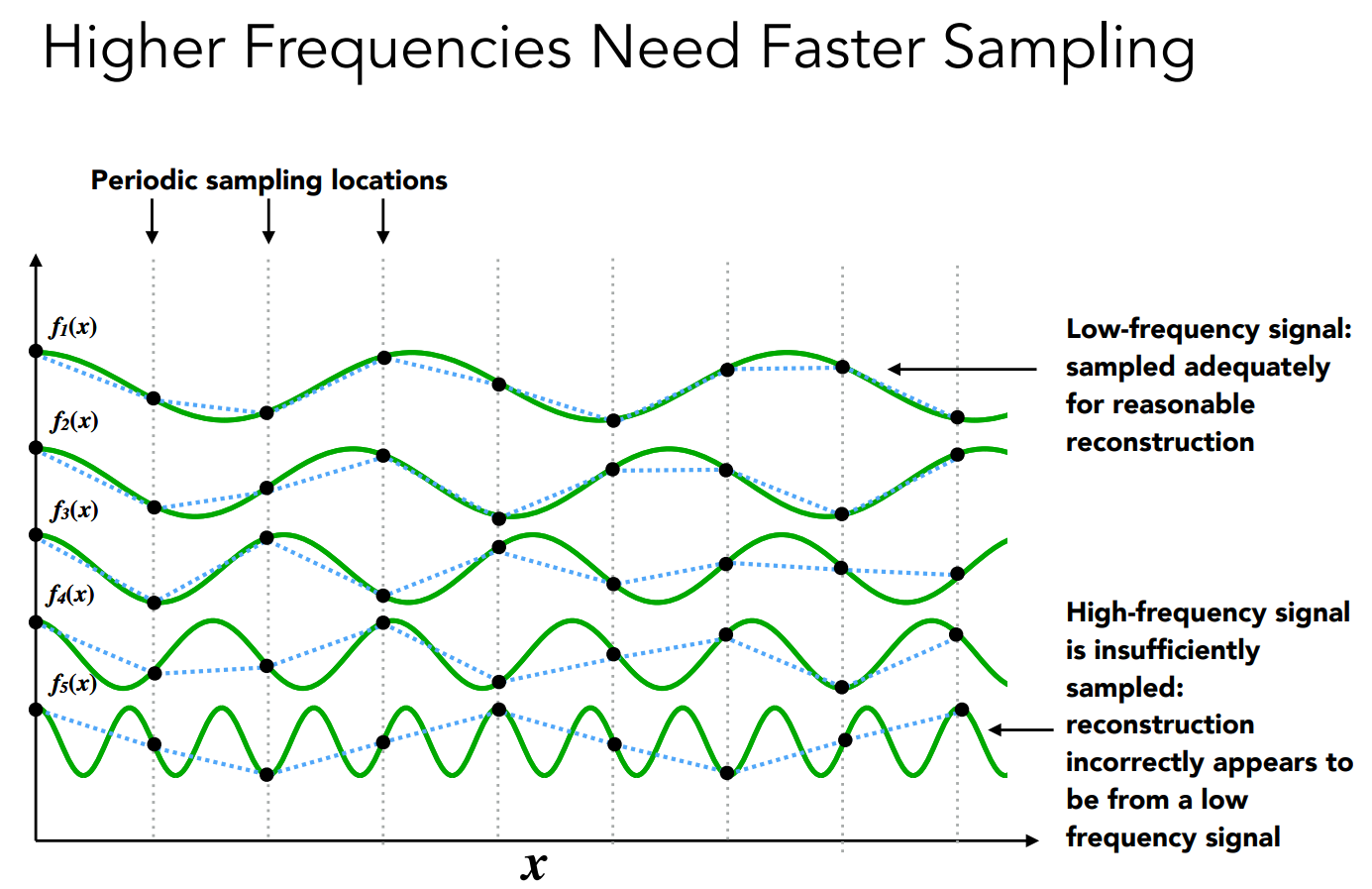
- 走样的定义:同样采样方法采样两种不同频率的函数无法区分它们
Filtering 滤波¶
- 解释:Getting rid of certain frequency contents (去掉一系列的频率)
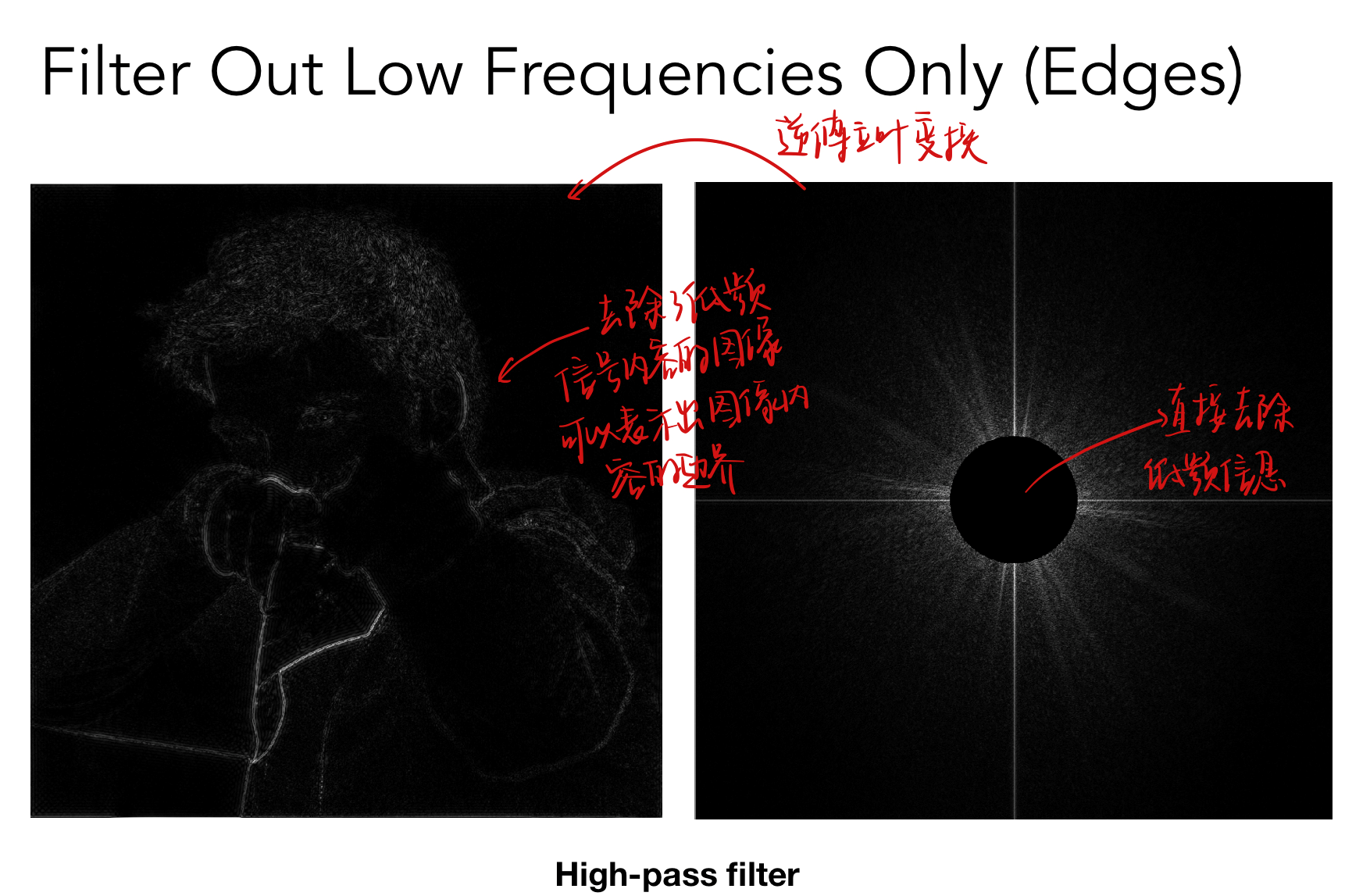
这是一个图像经过傅里叶变换后的频域图

在经过高通滤波(去掉低频信息)之后,可以提取出图像的边界
高频信息对应图像边界的理由:图像的边界的左右两侧发生了剧烈的变化,是高频信息
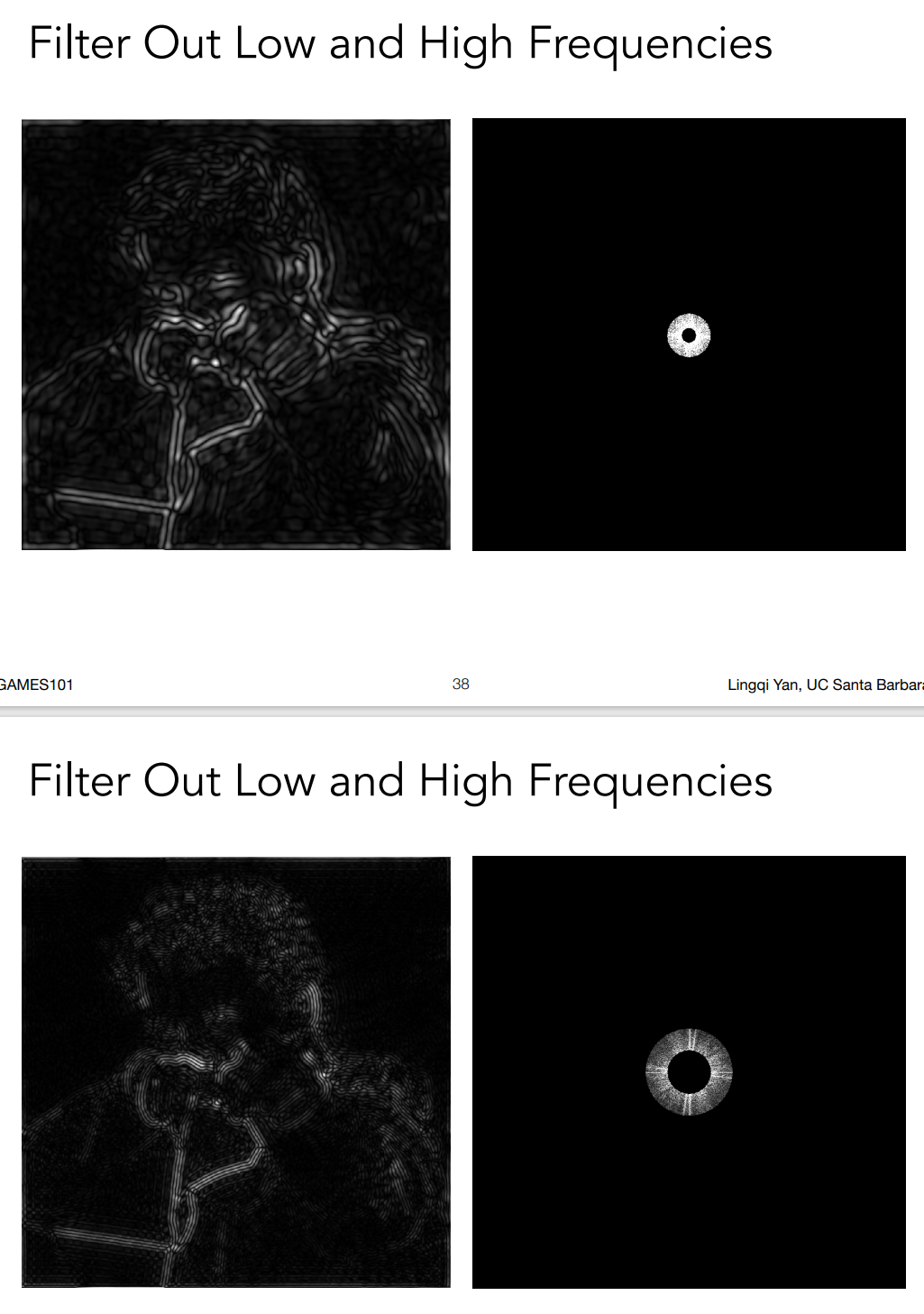
反之,低通滤波(去掉高频信息)就对应了边界被模糊的情况

如果留下某一段的频率,就留下的是一部分的边界信息
Convolution 卷积¶
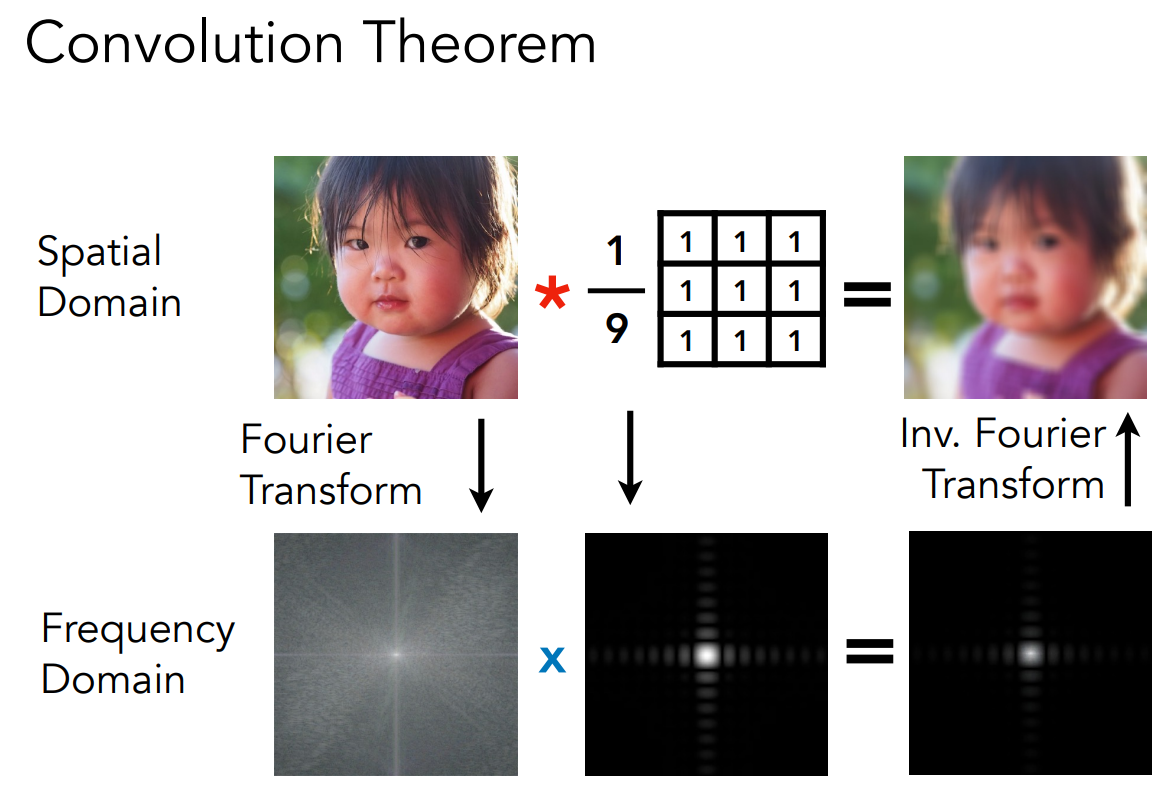
- Convolution in the spatial domain is equal to multiplication in the frequency domain, and vice versa
- 作用
- Option 1: Filter by convolution in the spatial domain
- Option 2:
- Transform to frequency domain (Fourier transform)
- Multiply by Fourier transform of convolution kernel
- Transform back to spatial domain (inverse Fourier)
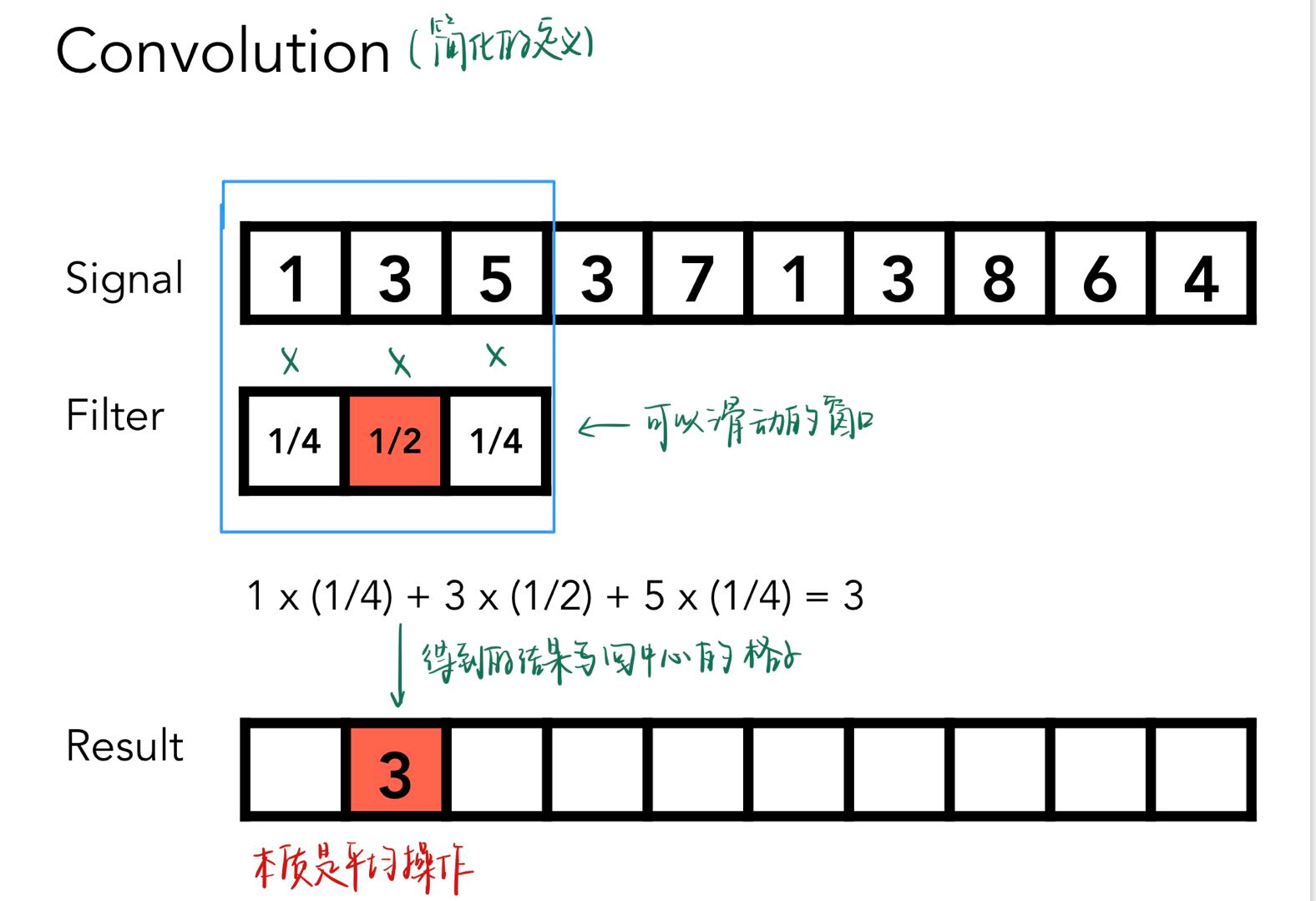
卷积定理的一个例子
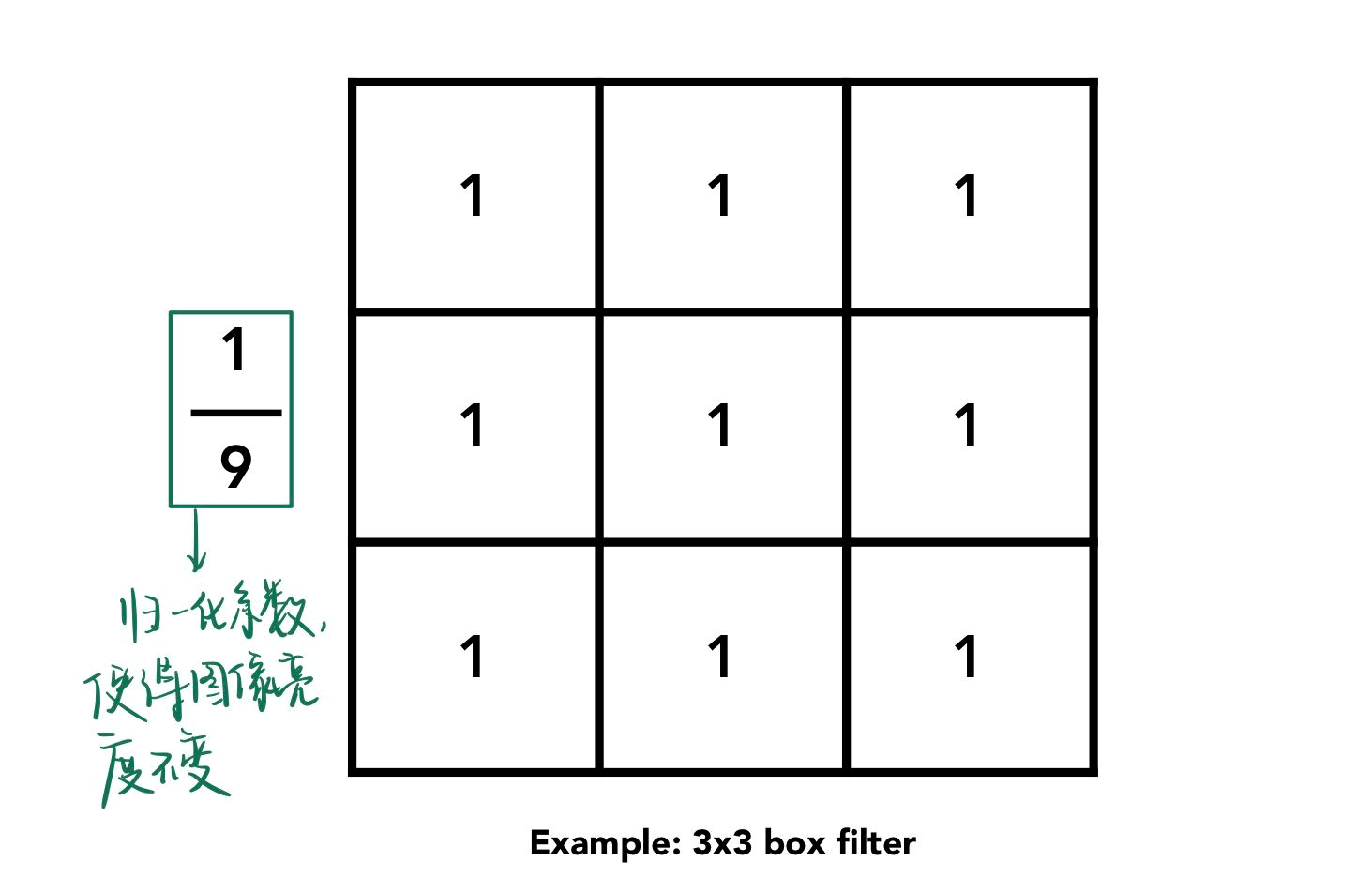
Box Filter 滤波盒¶


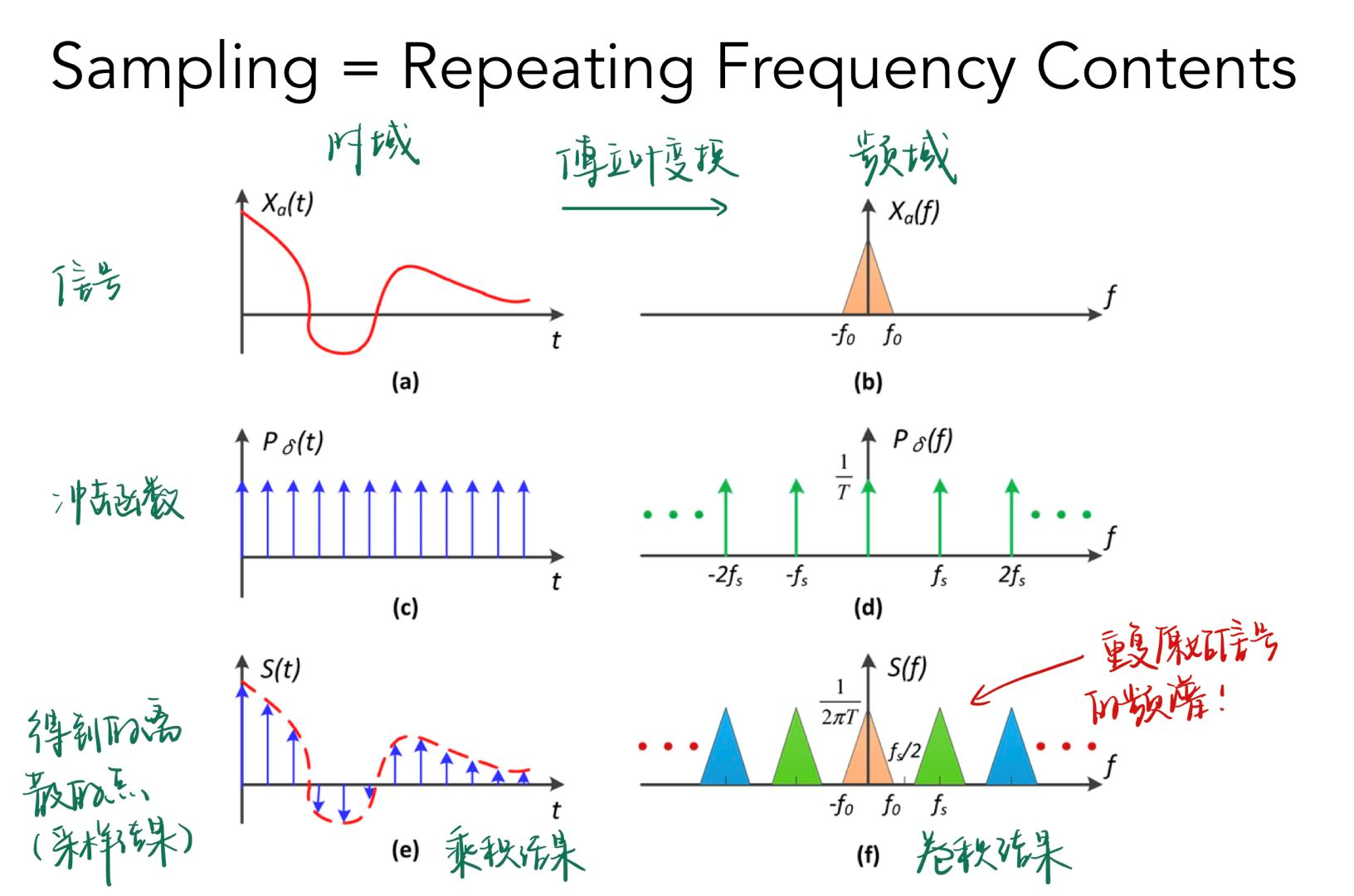
采样的本质¶
- Sampling = Repeating Frequency Contents
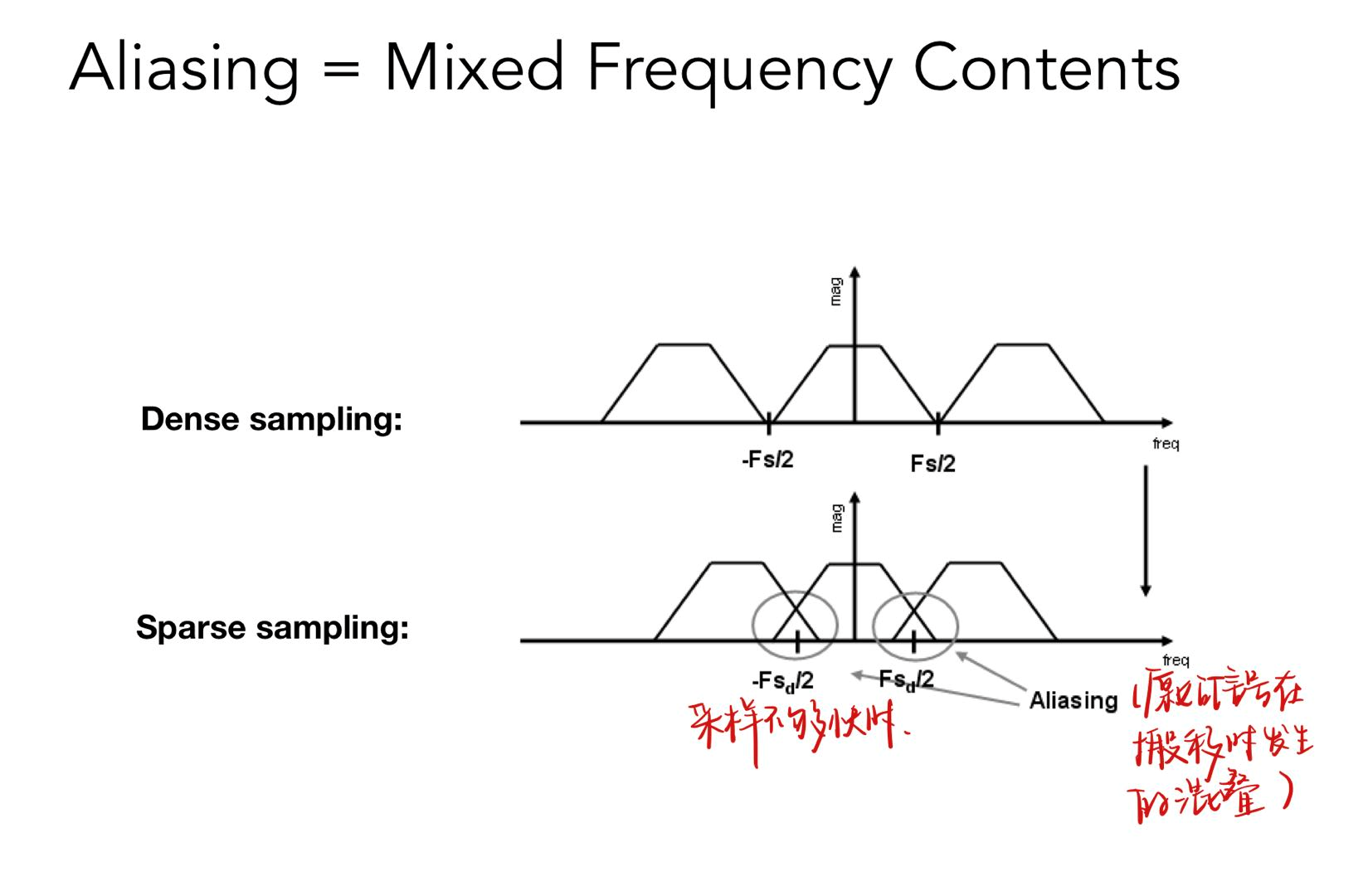
锯齿的本质¶
- Aliasing = Mixed Frequency Contents
Antialiasing 抗锯齿¶
抗锯齿的方法¶
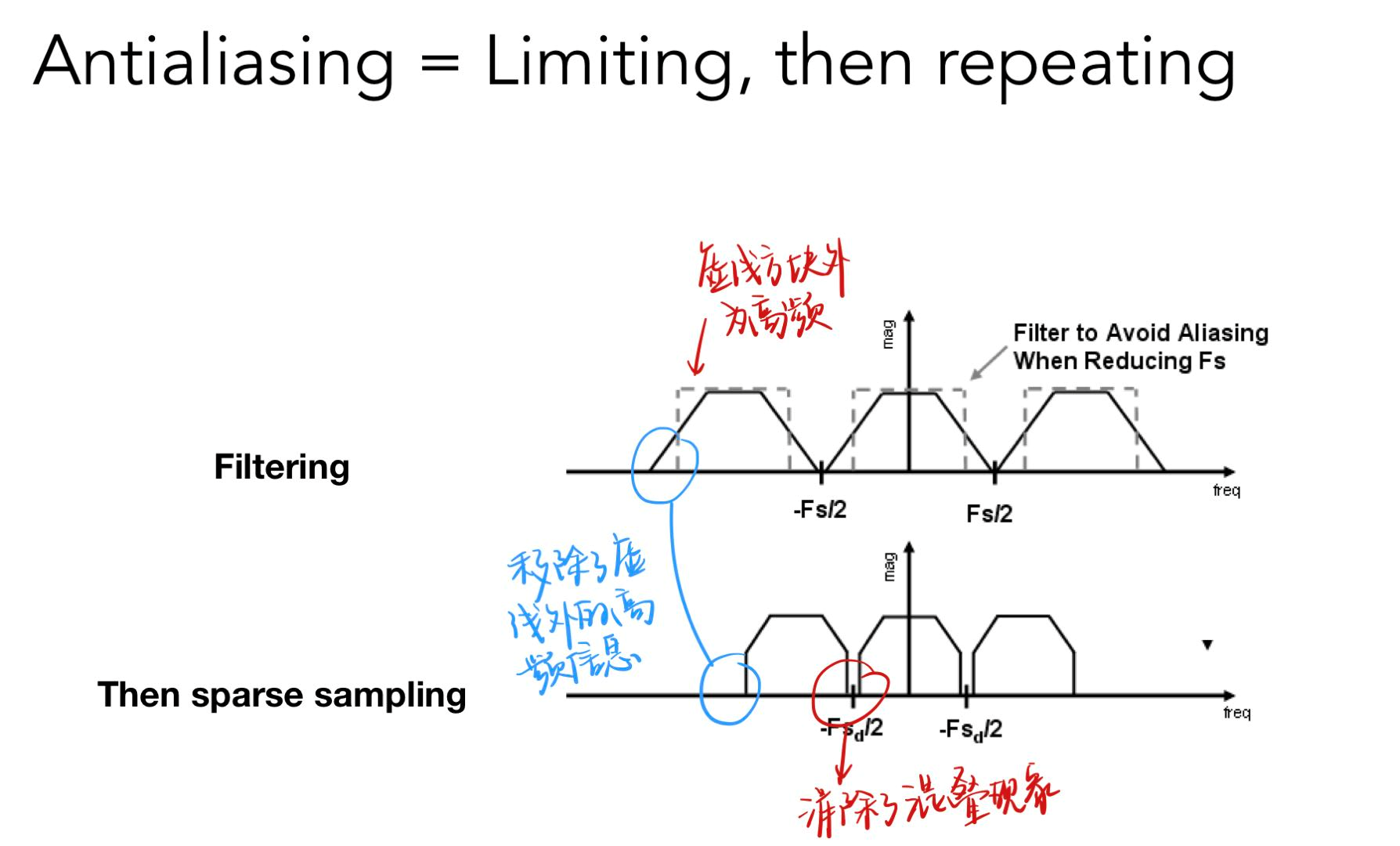
- 增加采样率:扩大频谱的搬移间隔
- 需要高分辨率显示设备
- 先做模糊(低通滤波),再做采样
反走样在像素层面的解决方案¶
-
求平均:Convolve \(f(x,y)\) by a 1-pixel box-blur
-
Recall: convolving = filtering = averaging
-
通过边界占像素的比例来觉得像素亮度从而完成模糊过程
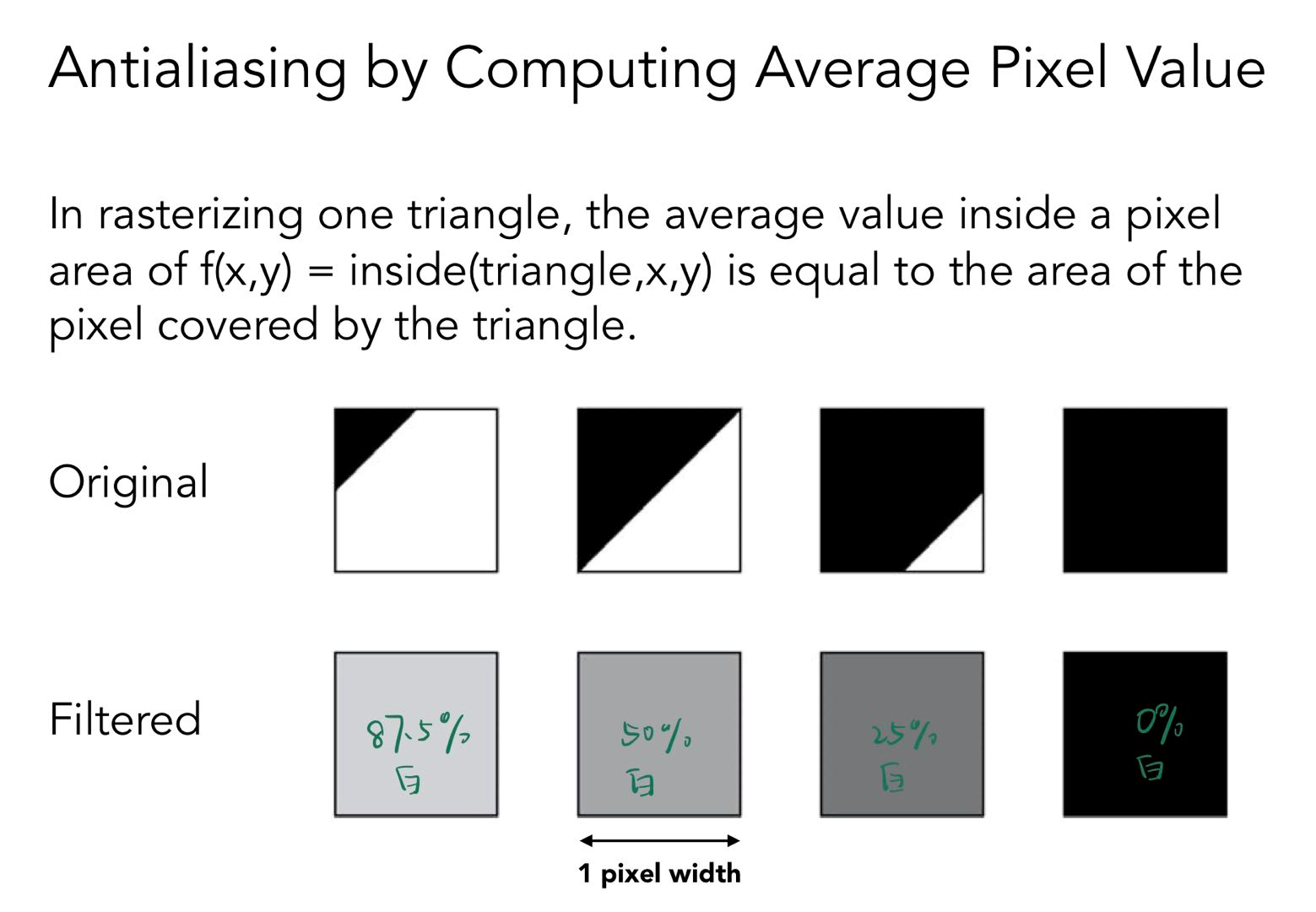
-
-
采样:Then sample at every pixel’s center
Antialiasing By Supersampling (MSAA)¶
- 这是一个近似反走样的操作,不能完全的实现反走样
- 这是一个对信号的模糊操作,不是真正的靠提升像素的分辨率来实现的
- 这个操作使用了更多的点对三角形是否在像素内进行了测试,增大了计算量(例如把一个像素分为 \(2\times 2\) 的方格就增大了 \(4\) 倍的计算量
MSAA 的步骤¶
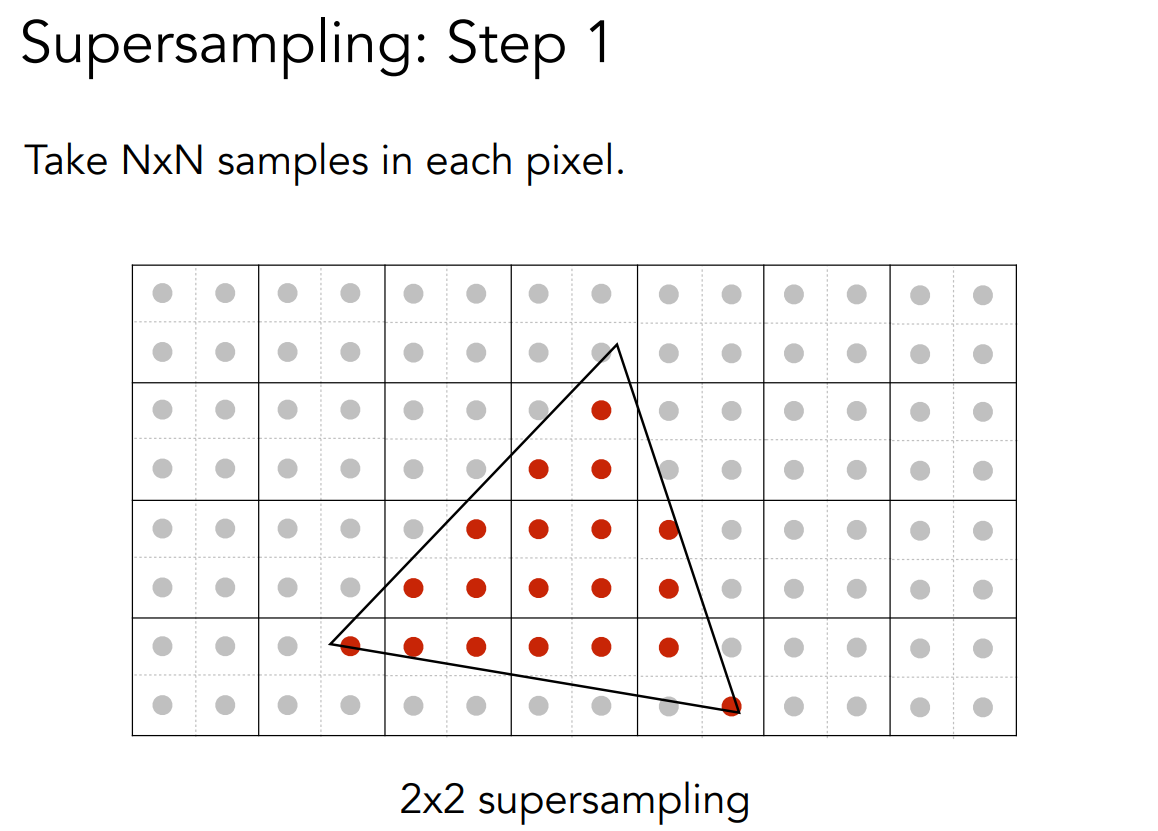
- Supersampling
将每个像素切分成 \(2\times 2\) 的方格,对方格中的每个点计算其是否在三角形内,根据每个像素在三角形内的点的个数决定发光的强度
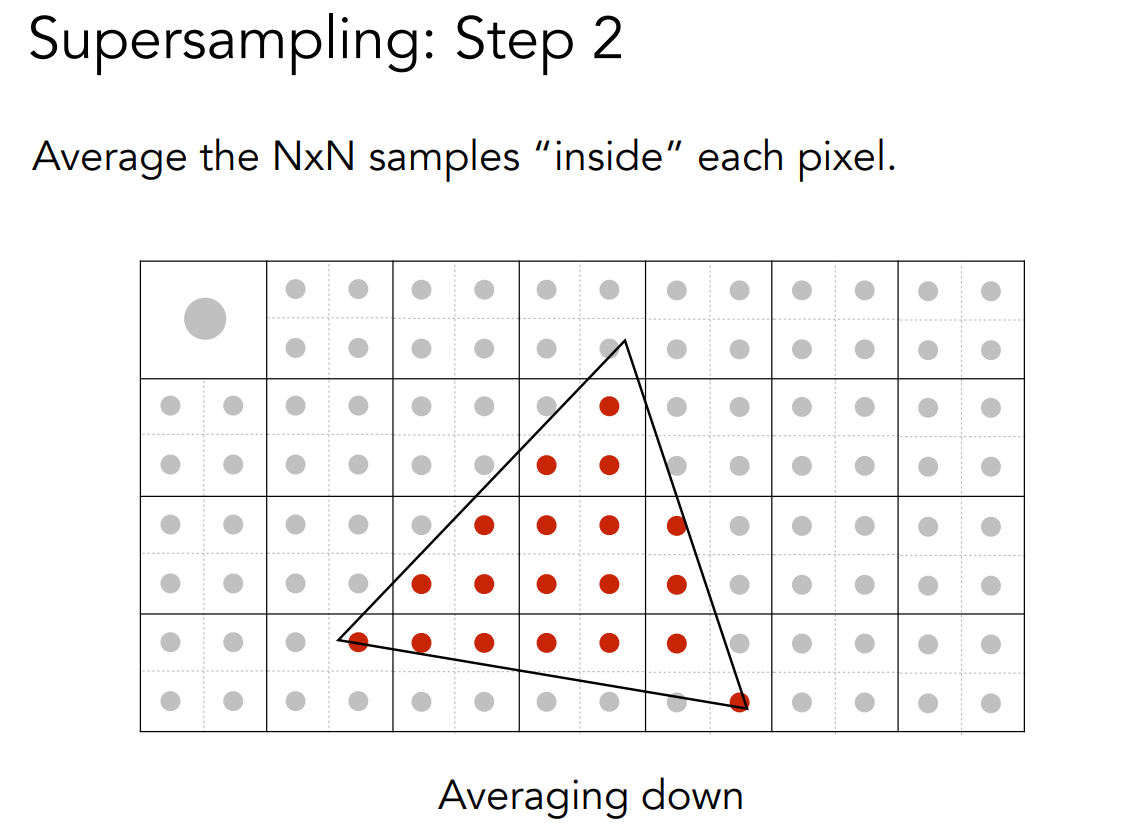
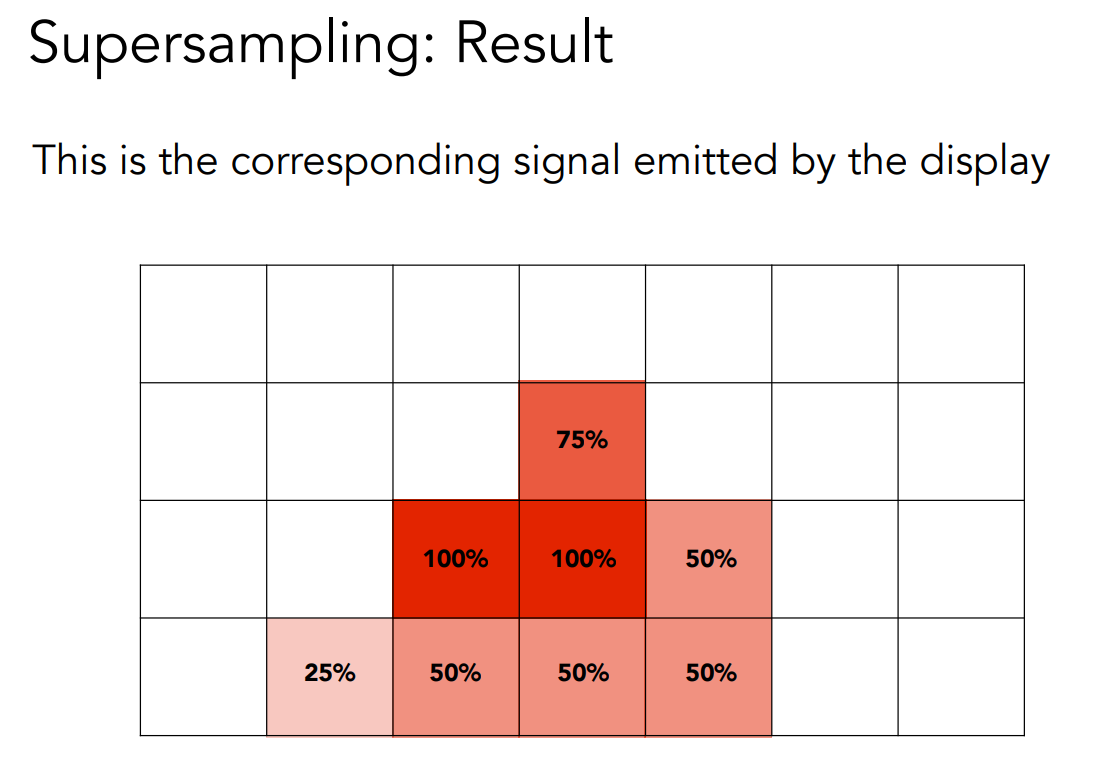
- Sampling
对图像根据模糊操作得到的值进行采样
更多的抗锯齿方法¶
- FXAA (Fast Approximate AA):本质的图像的后期处理,先得到有锯齿的图像,再将边界找到,将其换成没有锯齿的边界
- TAA (Temporal AA):去找上一帧的信息来进行模糊,如果是静态图片就用每一个像素内不同的点来感知边界,在当前帧上没有额外操作
- 超分辨率(与抗锯齿本质相同):使用深度学习猜测和补充细节
Z-Buffering 深度缓冲¶
Painter’s Algorithm 画家算法¶
- Paint from back to front, overwrite in the framebuffer
- Requires sorting in depth (\(O(n \log n)\) for \(n\) triangles)
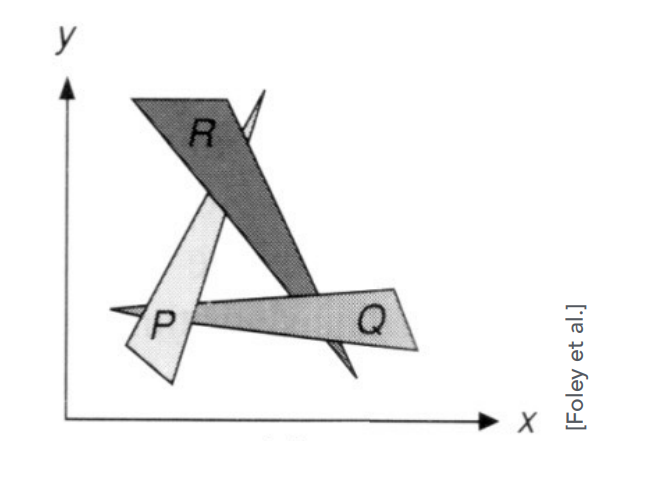
- Can have unresolvable depth order
- 如果两两存在覆盖关系,就无法定义深度顺序,如下图
Z-Buffer 深度缓存¶
-
现代使用的算法
-
Store current min. z-value for each sample (pixel) 此算法是针对像素的,操作针对像素,维护的是像素
-
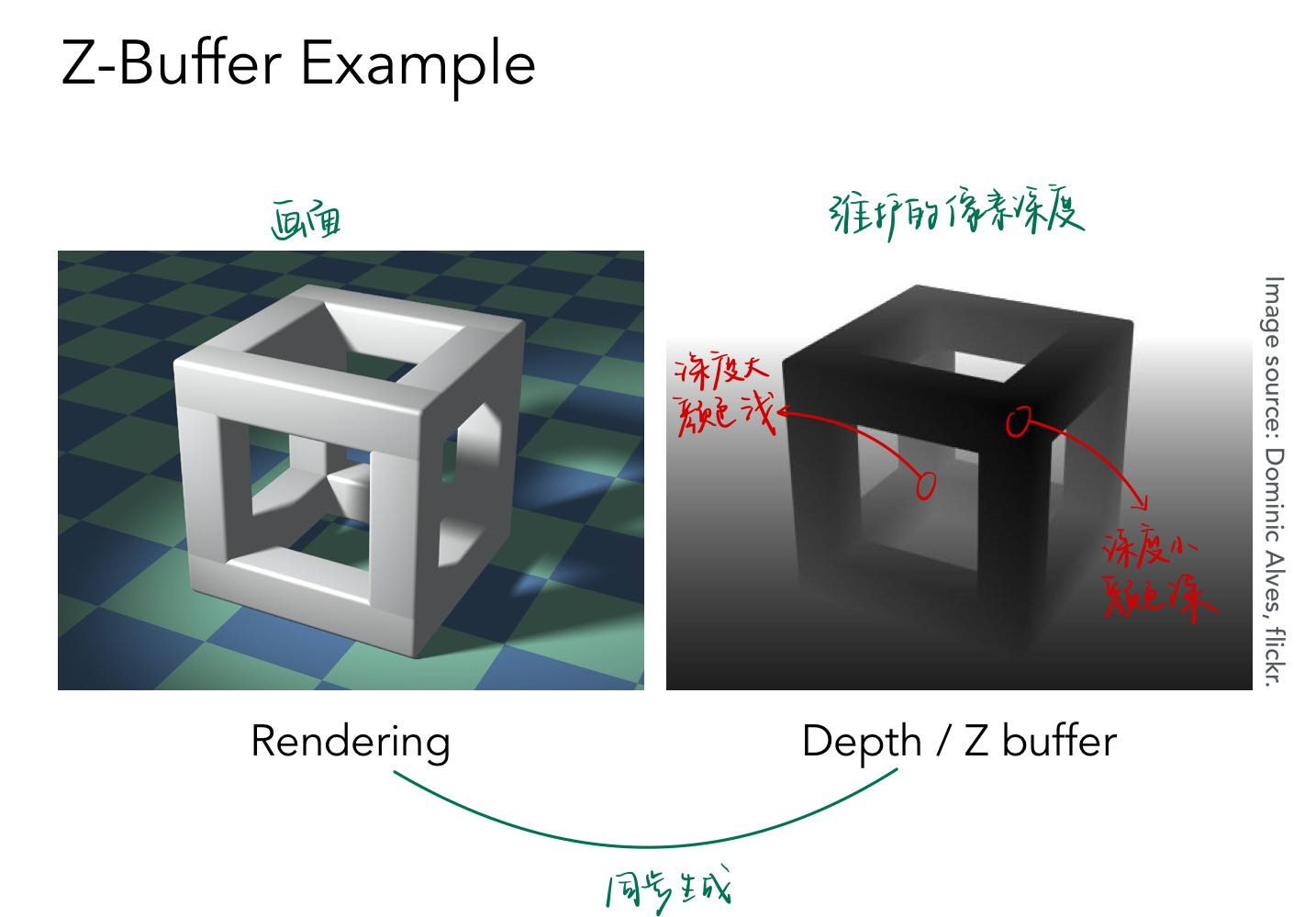
在生成图像时,同步生成两张图
-
frame buffer(最后的结果) stores color values
-
depth buffer (z-buffer 深度信息) stores depth
-
-
为了方便起见,假设
- z is always positive (smaller z \(\to\) closer, larger z \(\to\) further)
-
深度缓存算法和顺序无关(假设没有两个三角形在任何一个像素中没有相同深度,因为三角形的坐标基本都是使用浮点型存储,基本可以认为两个三角形没有相等的深度)
-
无法处理透明物体的深度
实际上,在生产环境还是有可能产生深度相同的情况,此课不讨论
深度缓存例子¶
算法流程¶

例如,第一个三角形的深度为 \(5\),更新 frame buffer, z-buffer。再叠加另一个三角形时,根据上述算法流程部分覆盖,这样第二个三角形的部分就会被遮挡
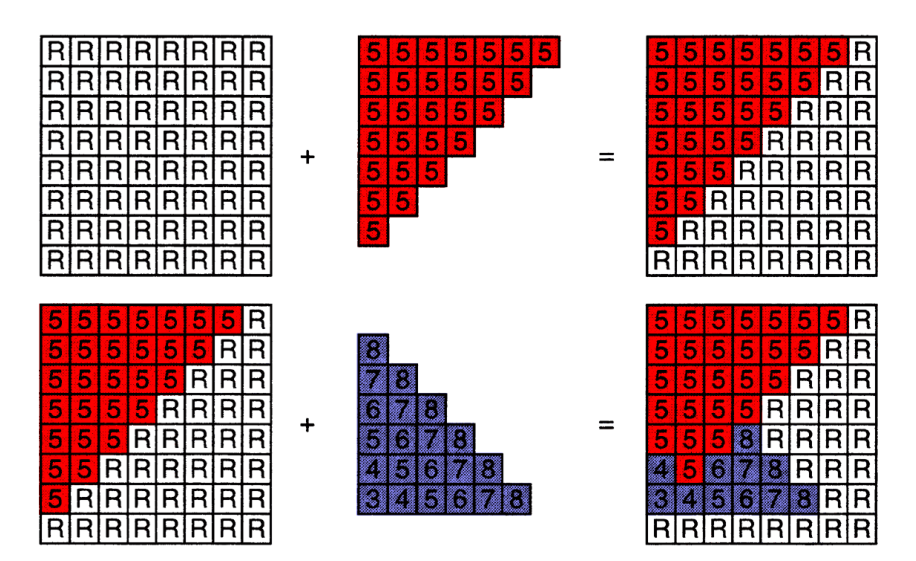
时间复杂度¶
假设一次操作,对于一个三角形而言的所要更新的像素为常数 \(C\) (通常在 \(100\) 个左右),时间复杂度为
- \(O(n)\) for \(n\) triangles (assuming constant coverage)
- 此处并没有排序,只是记录每个像素的最小值
Created: June 16, 2023