Lecture 05 Rasterization 1 (Triangles)¶

从规范立方体映射到屏幕¶

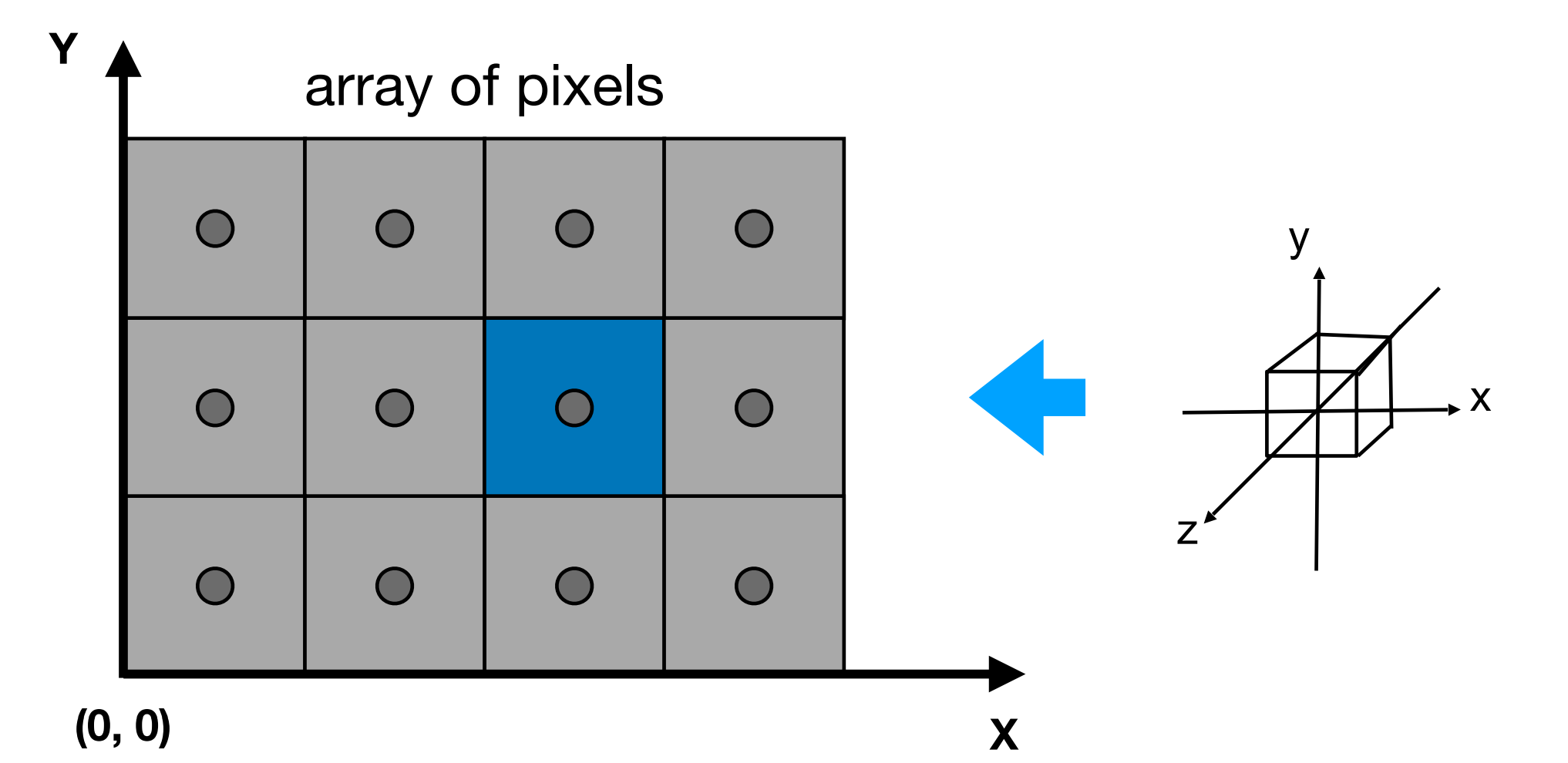
屏幕是像素构成的数组
数组的大小：分辨率
屏幕是一个典型的光栅成像设备
暂时认为像素是成像的最小单位

屏幕空间的定义¶

使用整数坐标描述像素
像素范围在 \((0,0)\) 到 \((width-1,height-1)\) 范围内
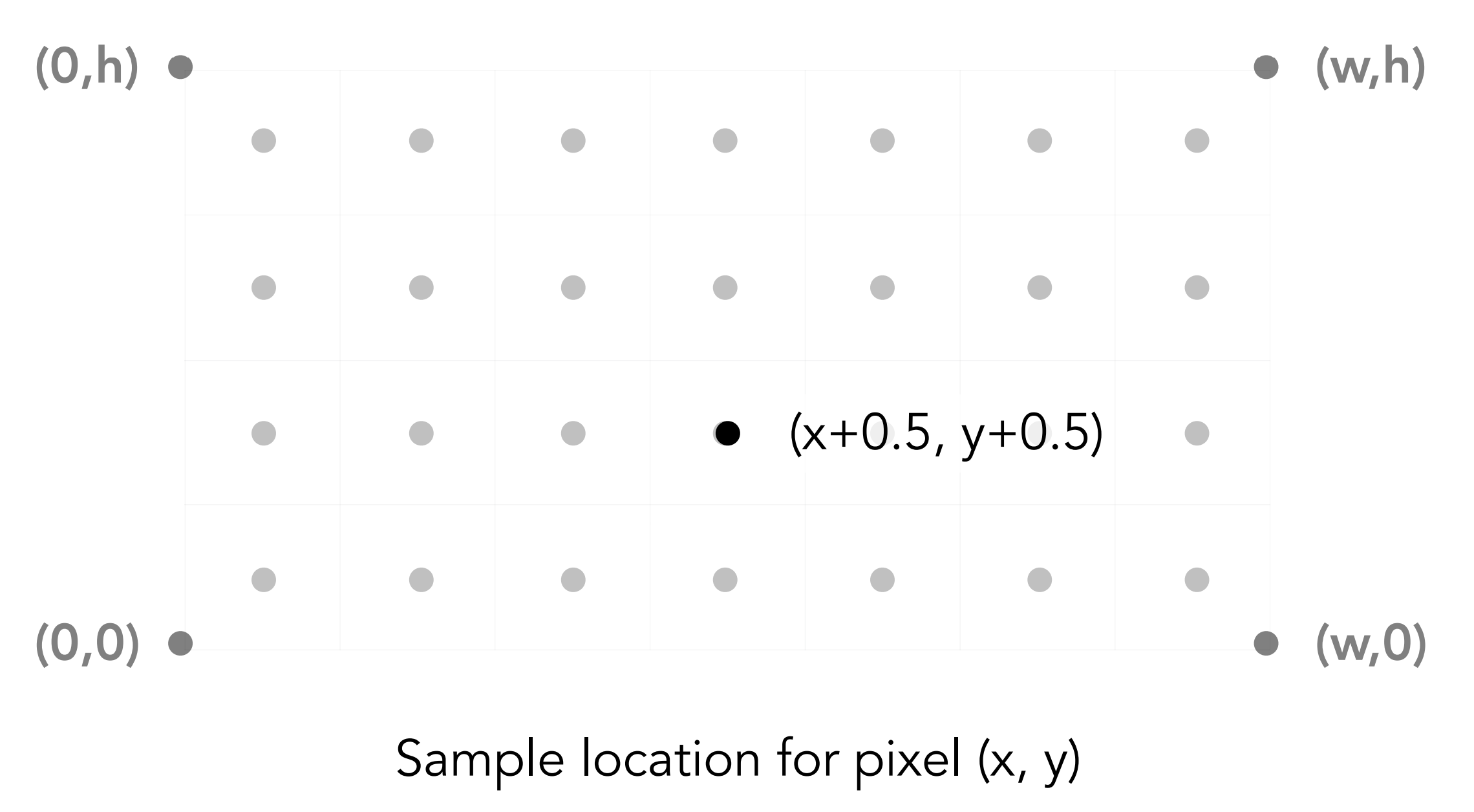
像素 \((x,y)\) 的中心坐标在 \((x+0.5,y+0.5)\)
整个屏幕的坐标范围在 \((0,0)\) 到 \((width,height)\) 之间

视口变换：将三维空间的立方体映射到屏幕¶

Irrelevant to \(z\)
Transform in \(xy\) plane: \([-1, 1]^2\) to \([0, width] \times [0, height]\)

视口变换矩阵

\[ M_{\text {viewport }}=\left(\begin{array}{cccc} \frac{w i d t h}{2} & 0 & 0 & \frac{\text { width }}{2} \\ 0 & \frac{\text { height }}{2} & 0 & \frac{\text { height }}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \]

Triangles - Fundamental Shape Primitives¶

使用三角形作为基本形状的原因¶

三角形是最基本的多边形
任何其他多边形都能被拆分为三角形
三角形的特有性质
- 三角形保证其在同一屏幕内（三点确定一个平面）
- 通过向量叉积可以轻松定义三角形的内部和外部（见 Lecture 2）
- 定义三角形顶点的属性可以轻松的在三角形内插值

Rasterization = Sampling A 2D Indicator Function¶

对三角形的光栅化的一个简单方式是对 2D 平面进行采样，采样的方式可以简单的通过函数描述如下

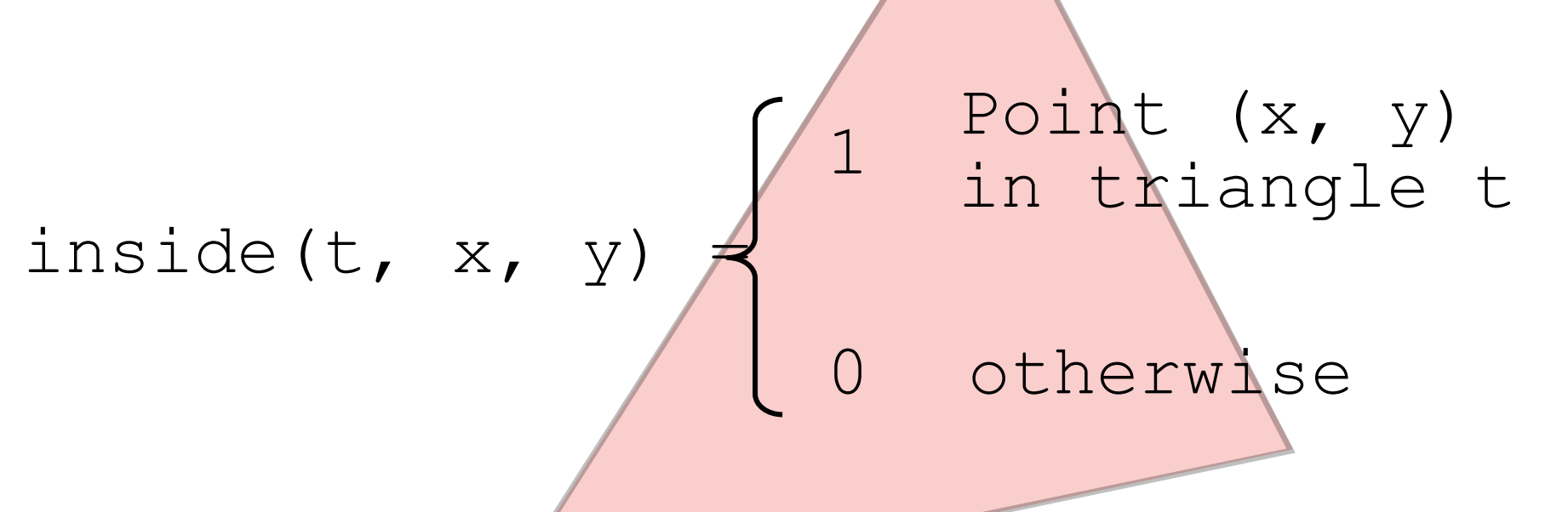
for (int x = 0; x < xmax; ++x) 
    for (int y = 0; y < ymax; ++y) 
        image[x][y] = inside(tri, x + 0.5, y + 0.5);

采样结束以后，再点亮屏幕中 image[x][y] = 1 的点即可，点的实际坐标是 \((x+0.5, y+0.5)\)

注意，采样不仅可以在位置上，可以在时间上进行采样，视频就是在时间中采样的一种方式

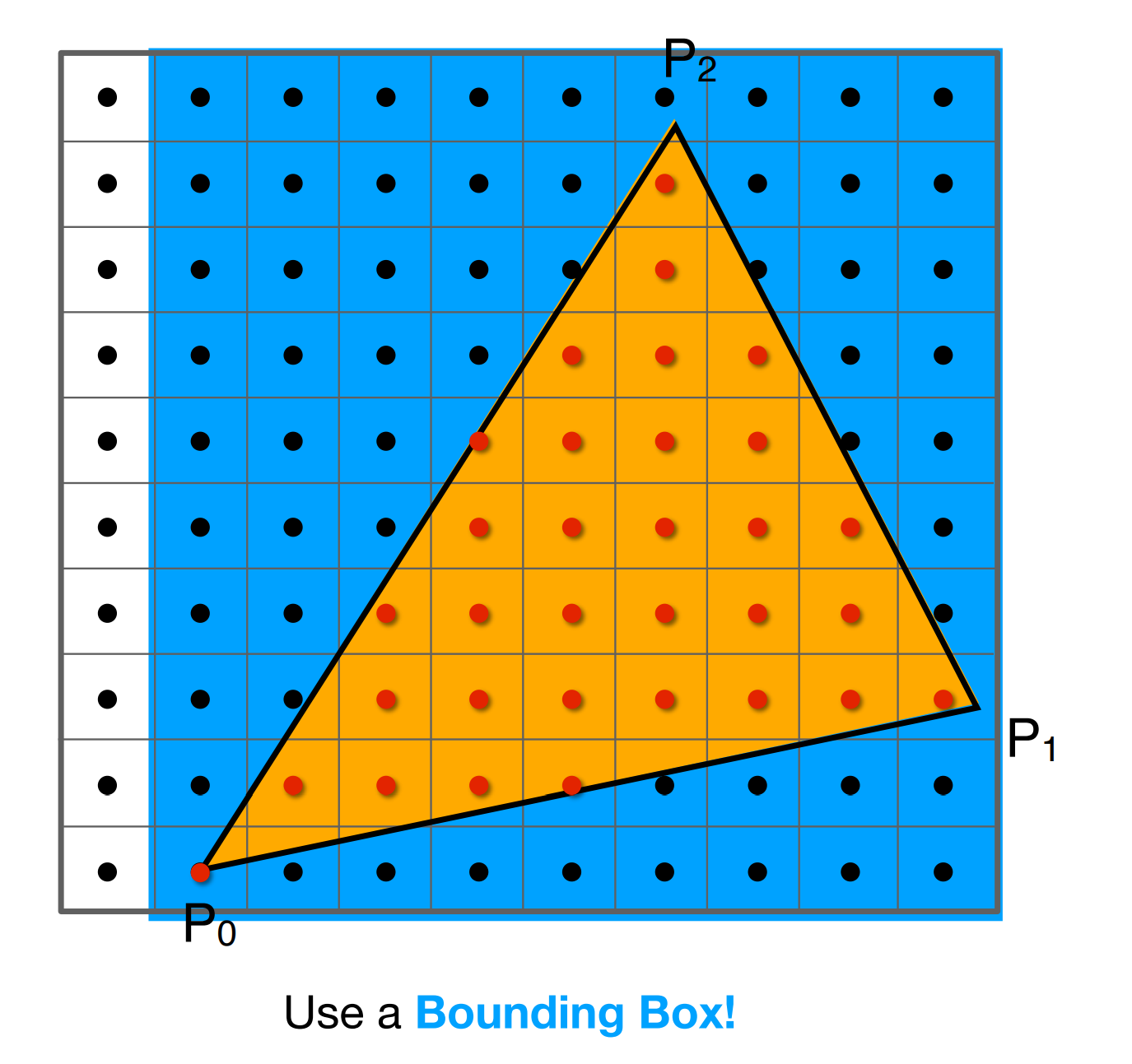
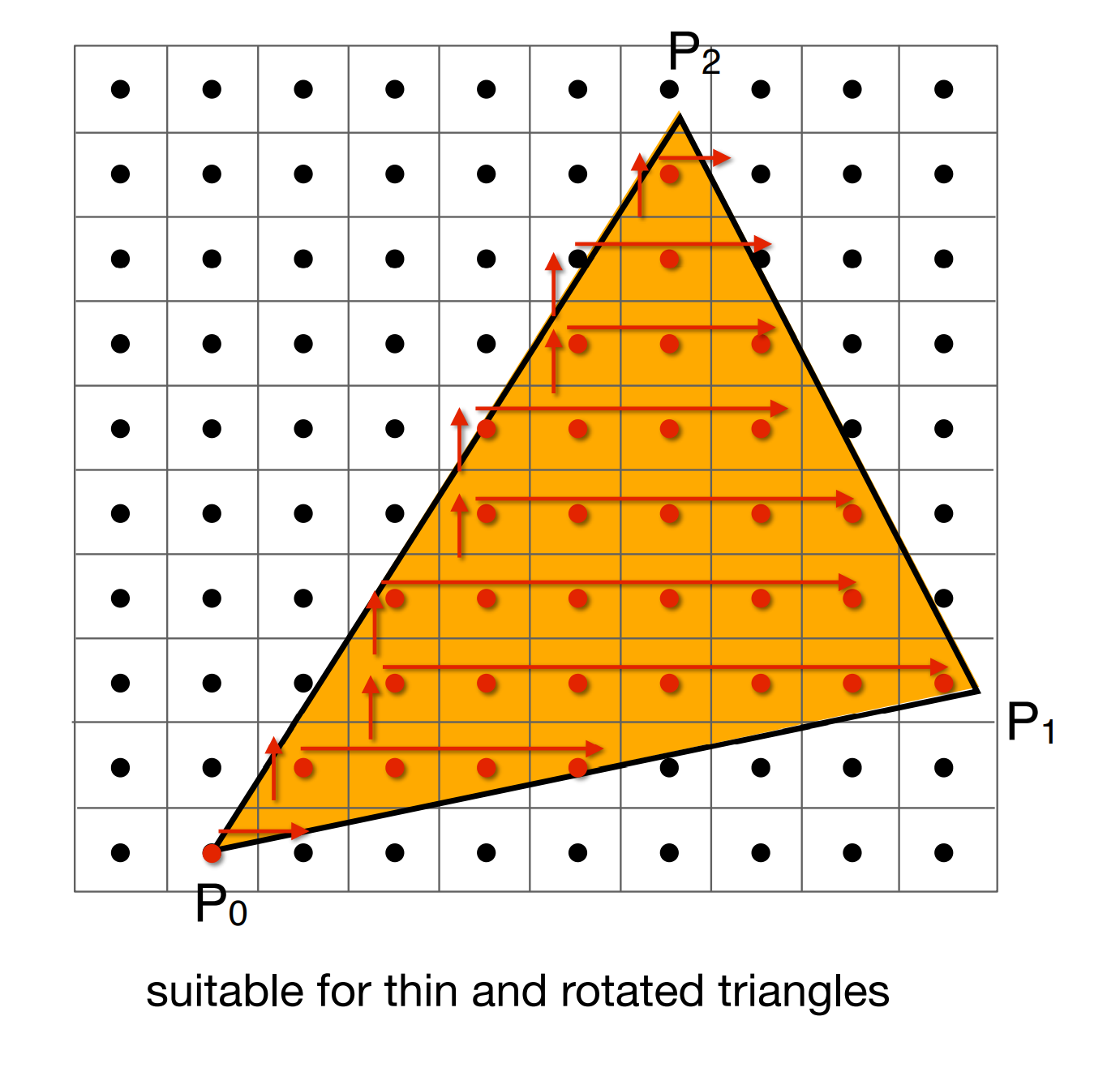
加速采样的方法
- 包围盒
- 进行增量三角形遍历：适合又瘦又长的三角形

Last update: July 30, 2023
Created: June 16, 2023