Lecture 03-04 Transformation¶

2D 线性变换¶

线性变换：变换能够用矩阵乘法得到

可以说，Linear Transformation = Matrices (of the same dimension)

我们将如下所示的简单矩阵乘法定义为对向量 $(x, y)^{T}$ 的线性变换。

\[ \left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} a_{11} x+a_{12} y \\ a_{21} x+a_{22} y \end{array}\right] \]

缩放 (scale)¶

缩放变换是一种沿着坐标轴作用的变换，定义如下:

\[ \operatorname{scale}\left(s_{x}, s_{y}\right)=\left[\begin{array}{cc} s_{x} & 0 \\ 0 & s_{y} \end{array}\right] \]

即除了 $(0,0)^{T}$ 保持不变之外，所有的点变为 $\left(s_{x} x, s_{y} y\right)^{T}$

剪切 (shearing)¶

shear 变换直观理解就是把物体一边固定，然后拉另外一边，定义如下:

\[ shear-x(s)=\left[\begin{array}{ll}1 & s \\ 0 & 1\end{array}\right], \\shear-y (s)=\left[\begin{array}{ll}1 & 0 \\ s & 1\end{array}\right] \]

拉向 $x$ 轴

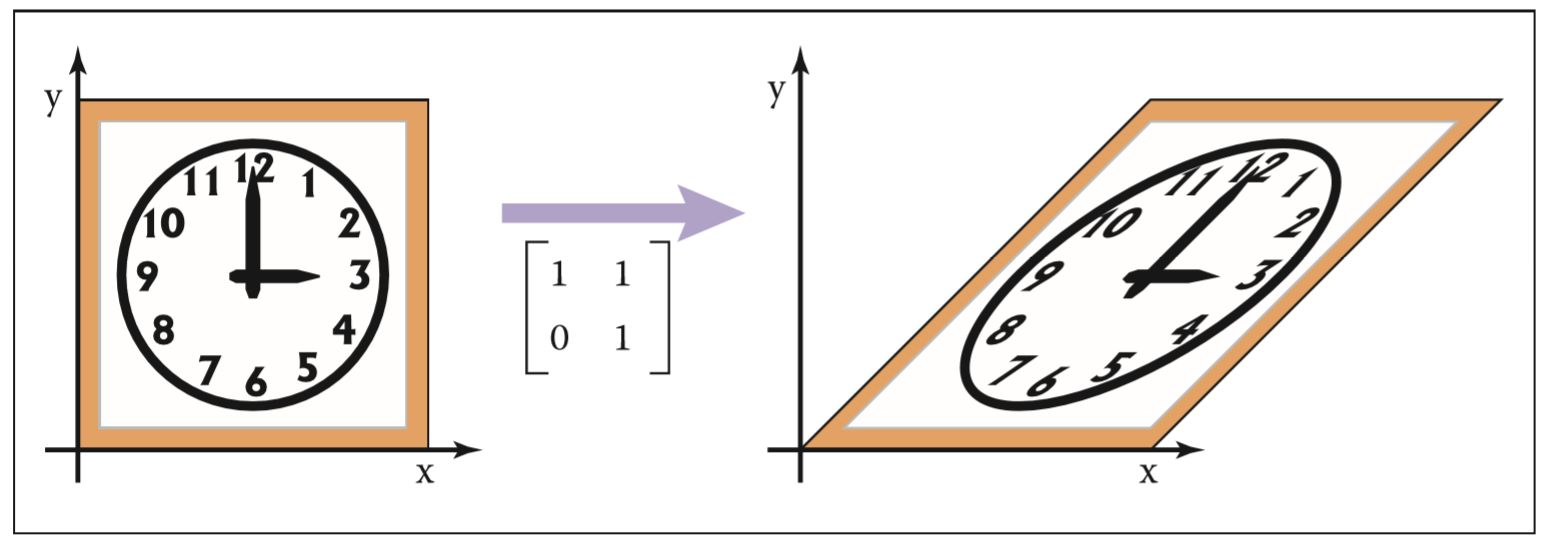
preview

拉向 $y$ 轴

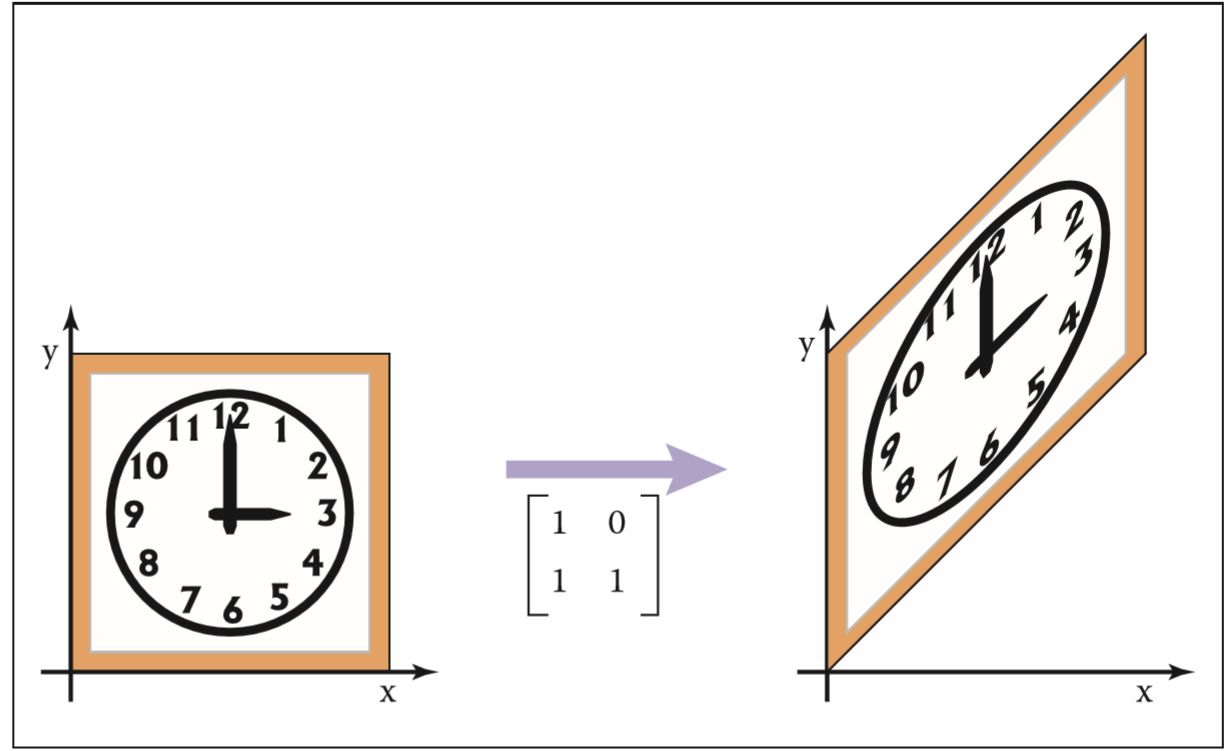
preview

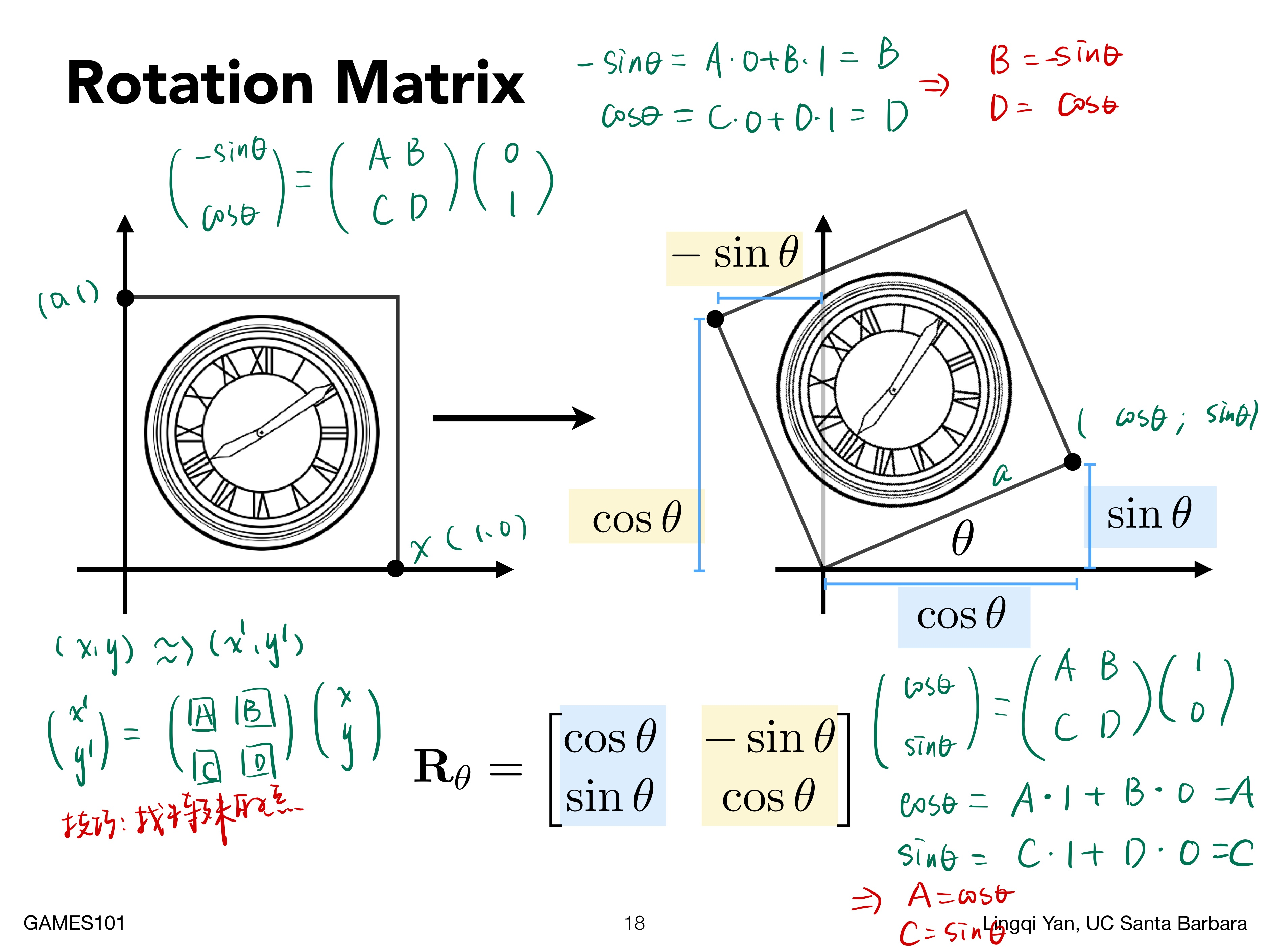
旋转 (rotation)¶

在无特殊说明的情况下，默认关于 $(0,0)$ 点，逆时针方向旋转 $\theta$ 角度（弧度）的公式如下

\[ \mathbf{R}_{\theta}=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right] \]

推导如下

齐次坐标¶

以上的线性变换矩阵不能描述平移变换，为了统一平移变换和线性变换（以上三种变换），引入平移变换

定义 2D 坐标和 2D向量如下

2D 坐标：$(x,y,1)^T$
2D 向量：$(x,y,0)^T$
- 由于向量具有平移不变性，第3维的0保护了向量不会因为平移而改变

齐次坐标下向量和点的操作¶

vector + vector = vector
point – point = vector
point + vector = point （一个点沿着向量移动）
point + point = 两个点的中点

此外，当第三维为 $w(w\ne 0)$时，定义

\[ \left(\begin{array}{c} x \\ y \\ w \end{array}\right) \text { is the } 2 \mathrm{D} \text { point }\left(\begin{array}{c} x / w \\ y / w \\ 1 \end{array}\right), w \neq 0 \]

仿射变换¶

仿射变换使用一个矩阵统一了所有操作
先应用线性变换再应用平移变换

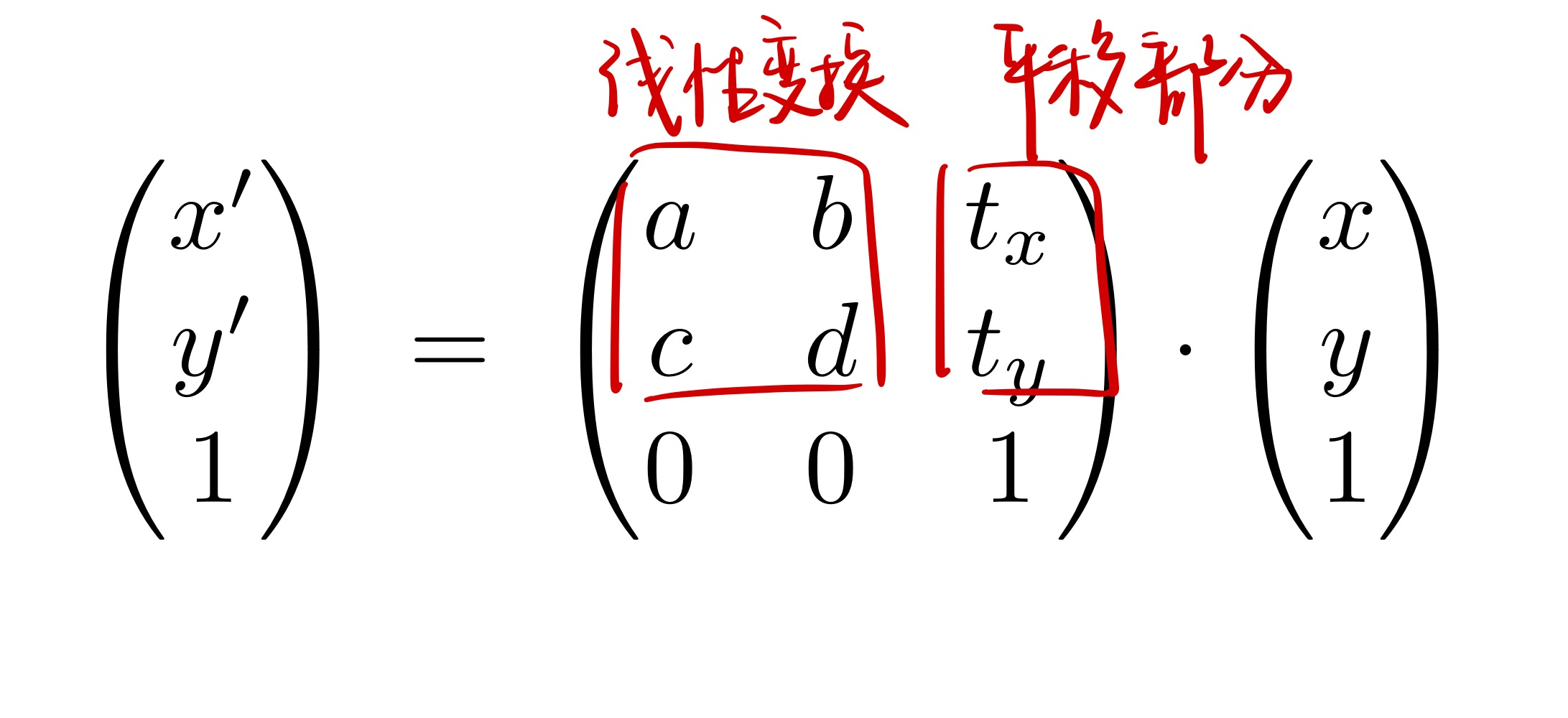
仿射变换下 2D 变换的描述¶

Scale¶

\[ \mathbf{S}\left(s_{x}, s_{y}\right)=\left(\begin{array}{ccc} s_{x} & 0 & 0 \\ 0 & s_{y} & 0 \\ 0 & 0 & 1 \end{array}\right) \]

Rotation¶

\[ \mathbf{R}(\alpha)=\left(\begin{array}{ccc} \cos \alpha & -\sin \alpha & 0 \\ \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 1 \end{array}\right) \]

Translation¶

\[ \mathbf{T}\left(t_{x}, t_{y}\right)=\left(\begin{array}{ccc} 1 & 0 & t_{x} \\ 0 & 1 & t_{y} \\ 0 & 0 & 1 \end{array}\right) \]

逆变换¶

使用逆矩阵
$\mathbf{M}^{-1}$ is the inverse of transform $\mathbf{M}$ in both a matrix and geometric sense

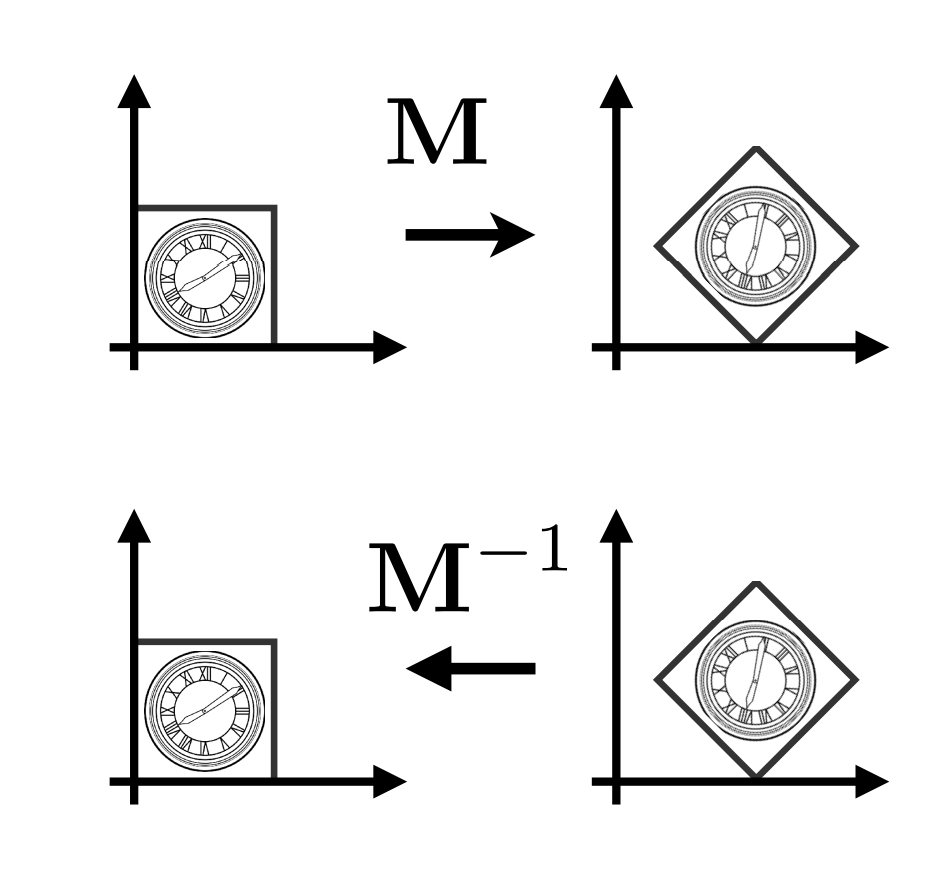
复合变换¶

复杂变换可由简单变换得到
变换的顺序非常重要，如先旋转再平移和先平移再旋转得到的结果不同
矩阵变换不满足交换律
计算是右结合的

3D 线性变换¶

再次使用齐次坐标描述

3D point $=(x, y, z, 1)^{T}$
3D vector $=(x, y, z, 0)^{T}$
In general, $(x, y, z, w)(w \ne0)$ is the 3D point: $(x / w, y / w, z / w)$
- e.g. $(1, 0, 0, 1)$ and $(2, 0, 0, 2)$ both represent $(1, 0, 0)$
先应用线性变换再应用平移变换

Use $4 \times 4$ matrices for affine transformations

\[ \left(\begin{array}{l} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ 1 \end{array}\right)=\left(\begin{array}{lllc} a & b & c & t_{x} \\ d & e & f & t_{y} \\ g & h & i & t_{z} \\ 0 & 0 & 0 & 1 \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right) \]

Scale¶

\[ \mathbf{S}\left(s_{x}, s_{y}, s_{z}\right)=\left(\begin{array}{cccc} s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \]

Translation¶

\[ \mathbf{T}\left(t_{x}, t_{y}, t_{z}\right)=\left(\begin{array}{cccc} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{array}\right) \]

? Rotation¶

around $x-, y-$, or $z$-axis
$\sin \alpha$ 的正负号由右手定则确定，顺序是 $x\to z$

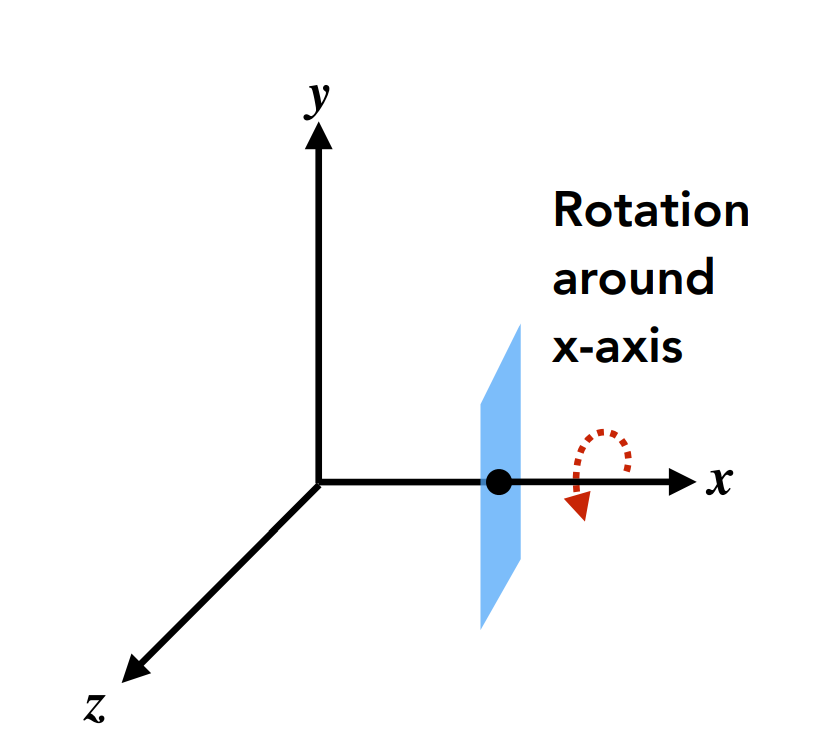
\[ \begin{aligned} \mathbf{R}_{x}(\alpha) &=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \\ \mathbf{R}_{y}(\alpha) &=\left(\begin{array}{cccc} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \\ \mathbf{R}_{z}(\alpha) &=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \end{aligned} \]

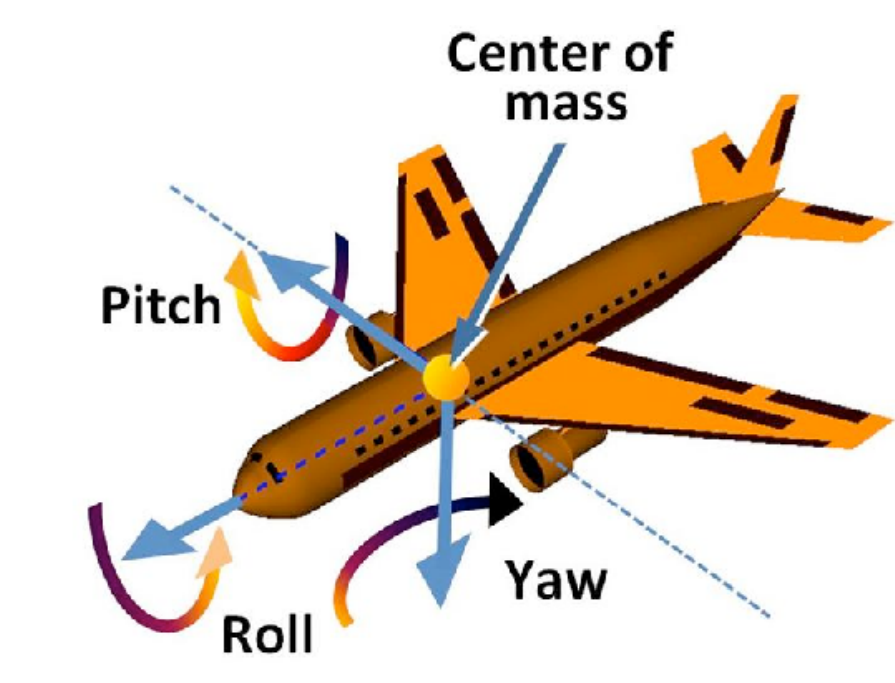
所有的 3D 变换都可以被描述为在 $x,y,z$ 轴上的旋转
- 也叫欧拉角
- Often used in flight simulators: roll, pitch, yaw

\[ \mathbf{R}_{x y z}(\alpha, \beta, \gamma)=\mathbf{R}_{x}(\alpha) \mathbf{R}_{y}(\beta) \mathbf{R}_{z}(\gamma) \]

Rodrigues’ Rotation Formula¶

Rotation by angle $\alpha$ around axis $n$

\[ \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha) \underbrace{\left(\begin{array}{ccc} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{array}\right)}_{\mathbf{N}} \]

View / Camera Transformation¶

Think about how to take a photo

Find a good place and arrange people (model transformation)
Find a good “angle” to put the camera (view transformation)
Cheese! (projection transformation 将三维空间投影到二维视图上）

Projection transformation¶

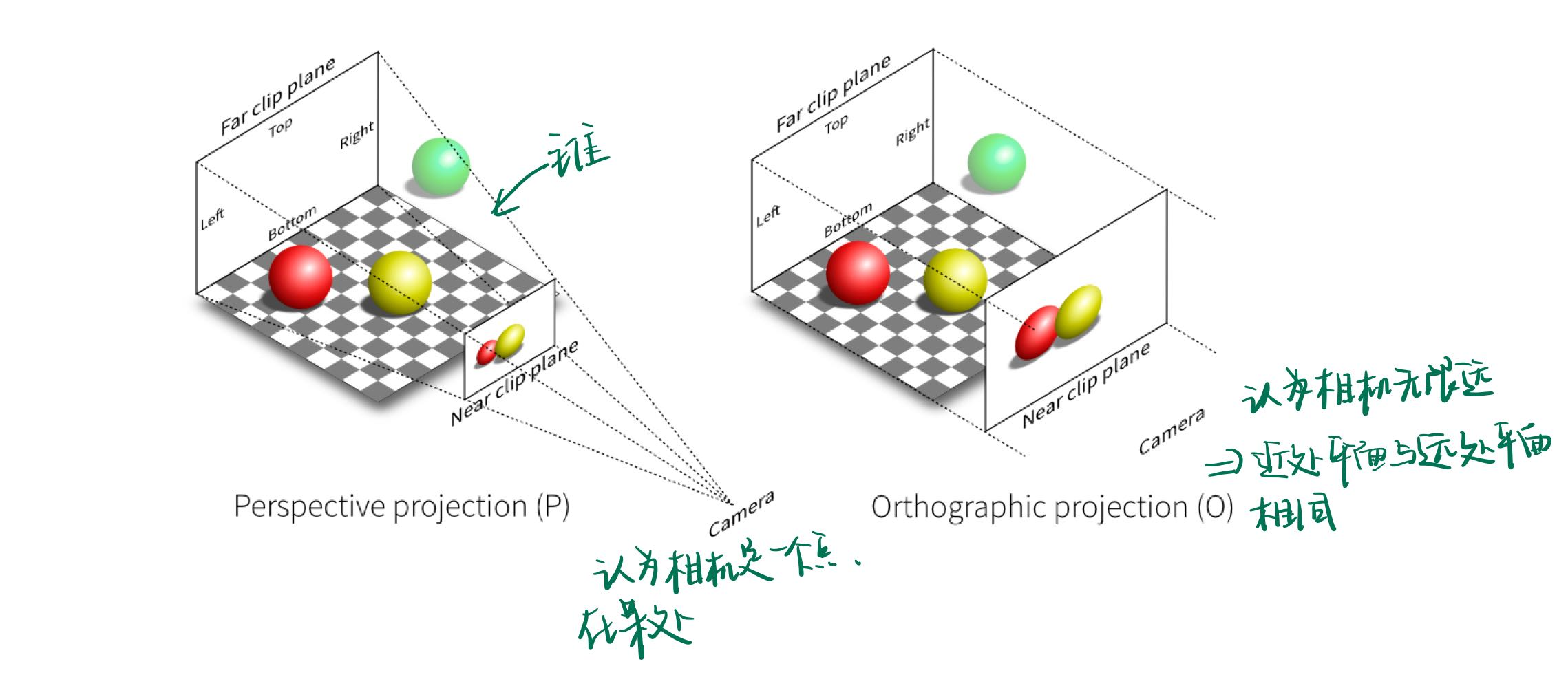
Orthographic projection¶

正则投影的步骤¶

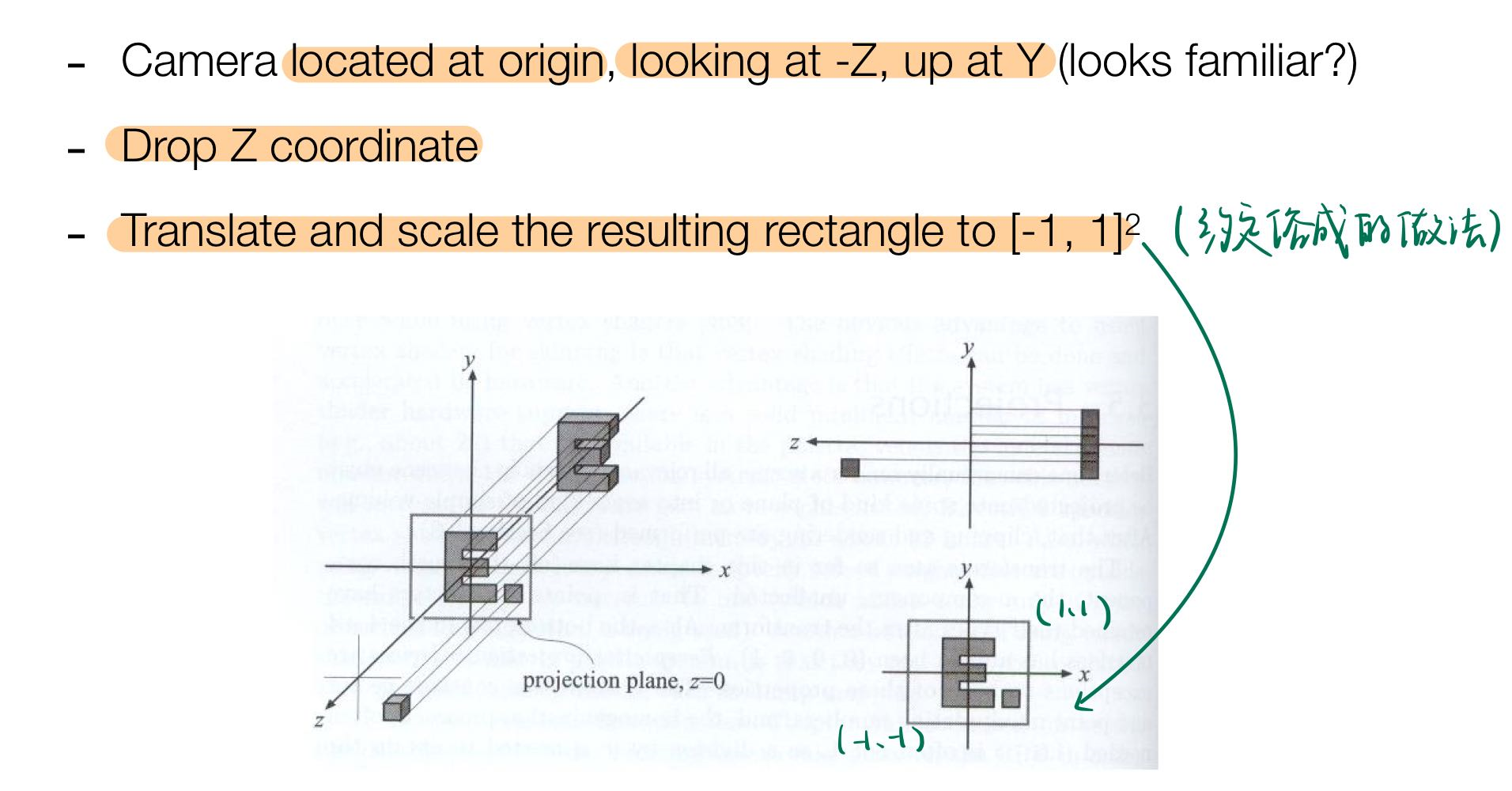
正则立方体¶

map a cuboid $[l, r] \times [b, t] \times [f, n]$ to the “canonical (正则、规范、标准)” cube $[-1, 1]^3$
- 因为是朝着 $z$ 轴负方向看，所以坐标小的是更远的 $f$ ，坐标大的是更近的 $n$

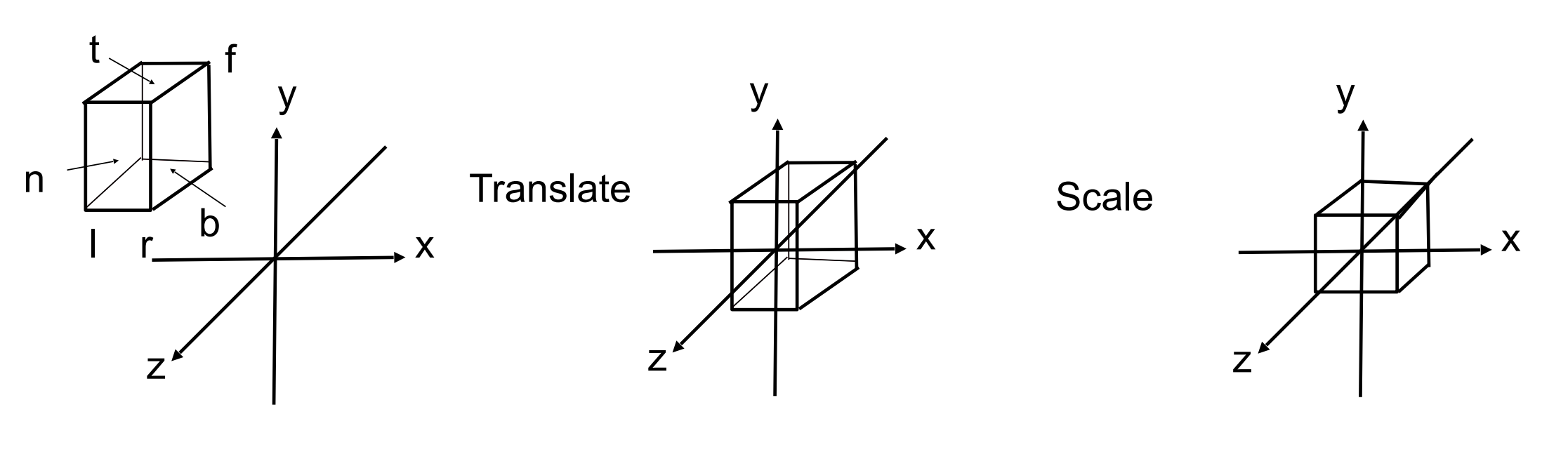
正则投影的变换矩阵¶

Translate (center to origin) first, then scale (length/width/height to 2)

\[ M_{\text {ortho }}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right] \]

Perspective projection¶

透视投影的步骤¶

First “squish” the frustum into a cuboid $(n \to n, f \to f) (M_{persp\to ortho})$ （将远平面挤压为与近平面相同的大小）
- 挤压规则
- 近平面永远不变，任何点在近平面上不变
- 远平面 $z$ 值不变，任何远平面上的点 $z$ 值不变
- 远平面的中心不变
Do orthographic projection ($M_{ortho}$) （做正则投影）

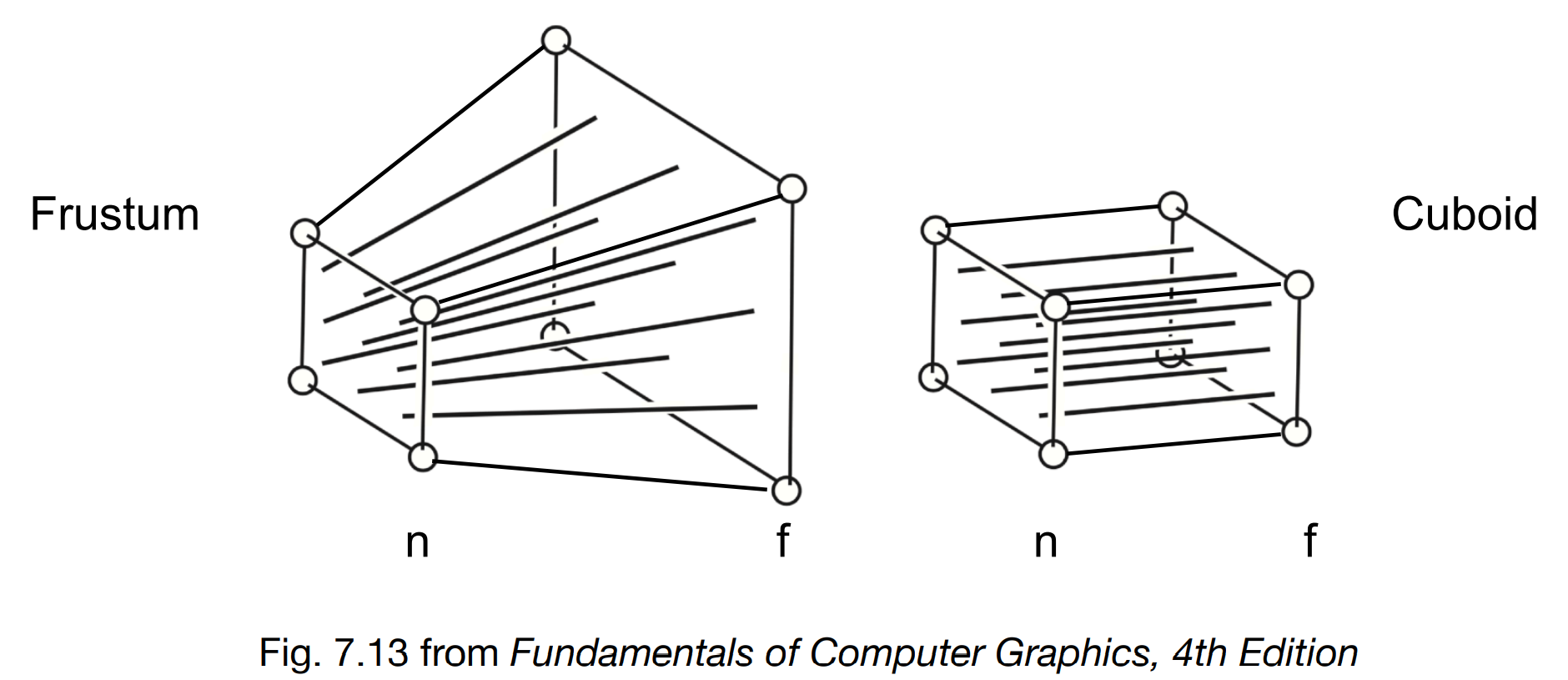
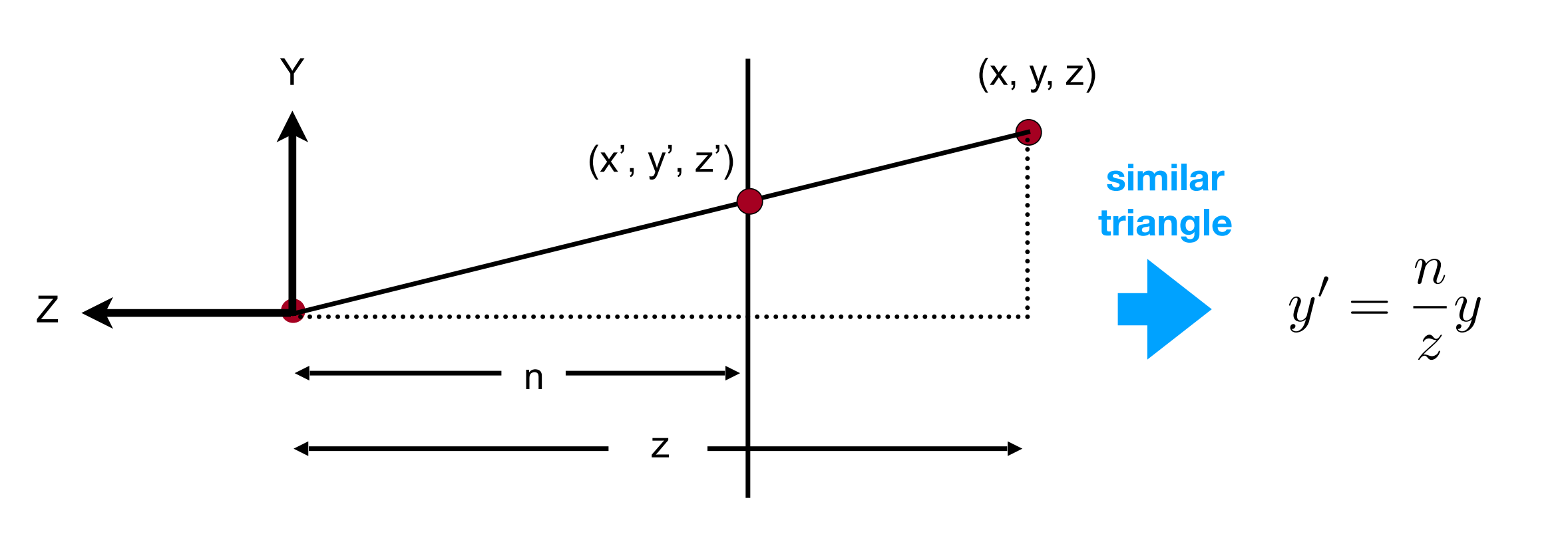
透视投影的变换矩阵推导¶

计算机图形学二：视图变换(坐标系转化，正交投影，透视投影，视口变换)

透视投影的变换矩阵¶

\[ \mathrm{M}_{\text {per }}=\mathrm{M}_{\text {ortho }} \mathrm{M}_{\text {persp } \rightarrow\text { ortho }} $$ $$ \mathrm{M}_{\text {per }}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -f n \\ 0 & 0 & 1 & 0 \end{array}\right] \]

Last update: July 30, 2023
Created: June 16, 2023