Skip to content

Lecture 02 Review of Linear Algebra

点乘

图形学中默认使用列向量

  • 二维
\[ \vec{a} \cdot \vec{b}=\left(\begin{array}{l} x_{a} \\ y_{a} \end{array}\right) \cdot\left(\begin{array}{l} x_{b} \\ y_{b} \end{array}\right)=x_{a} x_{b}+y_{a} y_{b} \]
  • 三维
\[ \vec{a} \cdot \vec{b}=\left(\begin{array}{c} x_{a} \\ y_{a} \\ z_{a} \end{array}\right) \cdot\left(\begin{array}{l} x_{b} \\ y_{b} \\ z_{b} \end{array}\right)=x_{a} x_{b}+y_{a} y_{b}+z_{a} z_{b} \]
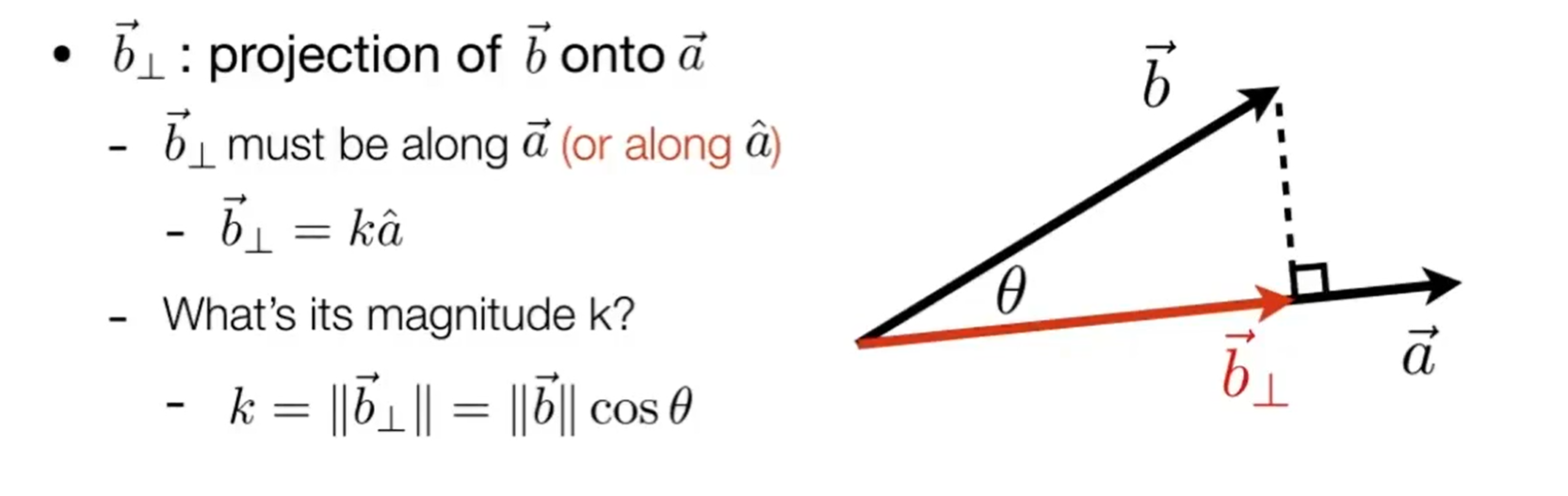
  • 作用
    • 找到两个向量间的夹角
    • 找到一个向量在另一个向量上的投影
    • 分解向量
    • 方向性：根据点乘的值 （\([-1,1]\)）

image-20220720120249756

叉积

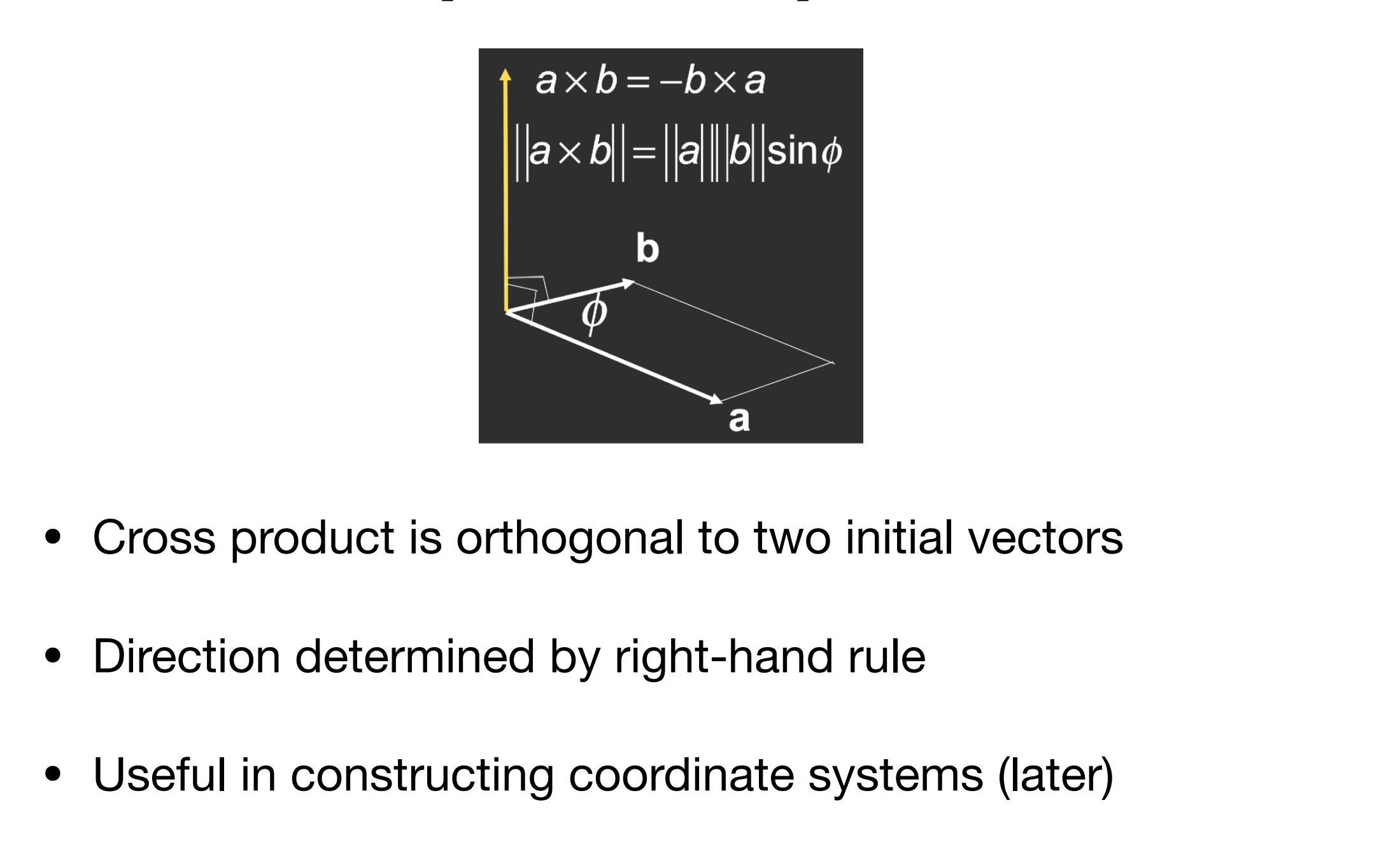
image-20220720122707966

\[ \vec{a} \times \vec{b}=\left(\begin{array}{c} y_{a} z_{b}-y_{b} z_{a} \\ z_{a} x_{b}-x_{a} z_{b} \\ x_{a} y_{b}-y_{a} x_{b} \end{array}\right) \]
  • Later in this lecture
\[ \vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc} 0 & -z_{a} & y_{a} \\ z_{a} & 0 & -x_{a} \\ -y_{a} & x_{a} & 0 \end{array}\right)\left(\begin{array}{l} x_{b} \\ y_{b} \\ z_{b} \end{array}\right) \]
  • 作用
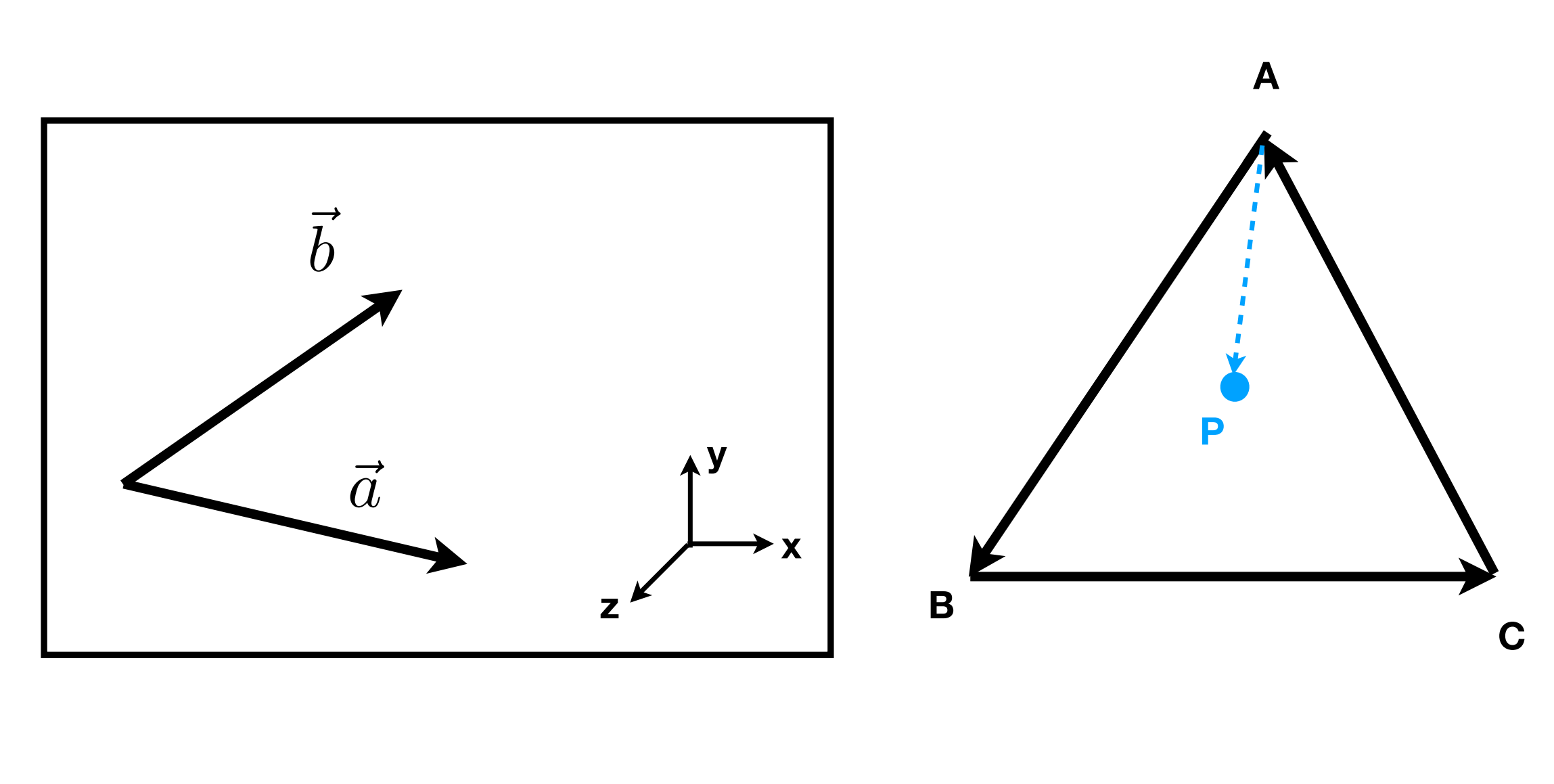
    • 判断向量的左右关系：
    • 叉积为正在左侧，否则在右侧
    • 判断一个点是否在三角形内：\(P\) 点在三条边的同侧（正负号相同）
    • Corner Case：结果为0，自己定义在内侧还是外侧

image-20220720122839106

正交坐标系

Any set of 3 vectors (in 3D) that

\[ \begin{aligned} &\|\vec{u}\|=\|\vec{v}\|=\|\vec{w}\|=1 \\ &\vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{w}=\vec{u} \cdot \vec{w}=0 \\ &\vec{w}=\vec{u} \times \vec{v} \quad \text { (right-handed) } \end{aligned} \]
  • 可以将任意一个向量分析到这三个轴上：投影方法
\[ \vec{p}=(\vec{p} \cdot \vec{u}) \vec{u}+(\vec{p} \cdot \vec{v}) \vec{v}+(\vec{p} \cdot \vec{w}) \vec{w} \]

矩阵

  • 矩阵乘法：需要算第几行第几列，就去找第几行第几列，把两个向量点乘起来

    • Element \((i, j)\) in the product is the dot product of row \(i\) from \(A\) and column \(j\) from \(B\)

    • 没有交换率

    • 有以下规律
    • \((AB)C=A(BC)\)
    • \(A(B+C) = AB + AC\)
    • \((A+B)C = AC + BC\)
    • 向量可以当作列矩阵

  • 矩阵转置

    • 交换行和列 \((ij \to ji)\)
    • 性质： \((A B)^{T}=B^{T} A^{T}\)
\[ \begin{gathered} \left(\begin{array}{ll} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{array}\right)^{T}=\left(\begin{array}{lll} 1 & 3 & 5 \\ 2 & 4 & 6 \end{array}\right) \\ \end{gathered} \]

  • 单位矩阵

    • 是一个对角阵，只有对角线上有非0元素

    • 来定义矩阵的逆

    \[ I_{3 \times 3}=\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) \]

  • 矩阵的逆

    • \(A A^{-1}=A^{-1} A=I\)
    • \((A B)^{-1}=B^{-1} A^{-1}\)

矩阵形式的向量点乘&叉乘操作

  • Dot product
\[ \begin{aligned} & \vec{a} \cdot \vec{b}=\vec{a}^{T} \vec{b} \\ =&\left(\begin{array}{lll} x_{a} & y_{a} & z_{a} \end{array}\right)\left(\begin{array}{l} x_{b} \\ y_{b} \\ z_{b} \end{array}\right)=\left(x_{a} x_{b}+y_{a} y_{b}+z_{a} z_{b}\right) \end{aligned} \]
  • Cross product
\[ \vec{a} \times \vec{b}=A^{*} b=\left(\begin{array}{ccc} 0 & -z_{a} & y_{a} \\ z_{a} & 0 & -x_{a} \\ -y_{a} & x_{a} & 0 \end{array}\right)\left(\begin{array}{l} x_{b} \\ y_{b} \\ z_{b} \end{array}\right) \]

PS：\(A^*\) ：dual matrix of vector \(\vec{a}\)

Last update: July 30, 2023
Created: June 16, 2023